Многие задачи приводят нас к поиску множества значений функции на некотором отрезке или на всей области определения. К таким задачам можно отнести различные оценки выражений, решение неравенств.
В этой статье дадим определение области значений функции, рассмотрим методы ее нахождения и подробно разберем решение примеров от простых к более сложным. Весь материал снабдим графическими иллюстрациями для наглядности. Так что эта статья является развернутым ответом на вопрос как находить область значений функции.
Определение.
Множеством значений функции y = f(x) на интервале X называют множество всех значений функции, которые она принимает при переборе всех .
Определение.
Областью значений функции y = f(x) называется множество всех значений функции, которые она принимает при переборе всех x из области определения .
Область значений функции обозначают как E(f) .
Область значений функции и множество значений функции - это не одно и то же. Эти понятия будем считать эквивалентными, если интервал X при нахождении множества значений функции y = f(x) совпадает с областью определения функции.
Не путайте также область значений функции с переменной x для выражения, находящегося в правой части равенства y=f(x) . Область допустимых значений переменной x для выражения f(x) – это есть область определения функции y=f(x) .
На рисунке приведены несколько примеров.
Графики функций показаны жирными синими линиями, тонкие красные линии – это асимптоты, рыжими точками и линиями на оси Оy изображена область значений соответствующей функции.
Как видите, область значений функции получается, если спроецировать график функции на ось ординат. Она может быть одним единственным числом (первый случай), множеством чисел (второй случай), отрезком (третий случай), интервалом (четвертый случай), открытым лучом (пятый случай), объединением (шестой случай) и т.п.
Так что же нужно делать для нахождения области значений функции.
Начнем с самого простого случая: покажем как определять множество значений непрерывной функции y = f(x) на отрезке .
Известно, что непрерывная на отрезке функция достигает на нем своего наибольшего и наименьшего значений . Таким образом, множеством значений исходной функции на отрезке
будет отрезок 
. Следовательно, наша задача сводится к нахождению наибольшего и наименьшего значения функции на отрезке .
Для примера найдем область значений функции арксинуса.
Пример.
Укажите область значений функции y = arcsinx .
Решение.
Областью определения арксинуса является отрезок [-1; 1]
. Найдем наибольшее и наименьшее значение функции на этом отрезке.
Производная положительна для всех x
из интервала (-1; 1)
, то есть, функция арксинуса возрастает на всей области определения. Следовательно, наименьшее значение она принимает при x = -1
, а наибольшее при x = 1
.
Мы получили область значений функции арксинуса 
.
Пример.
Найдите множество значений функции 
на отрезке
.
Решение.
Найдем наибольшее и наименьшее значение функции на данном отрезке.
Определим точки экстремума, принадлежащие отрезку
:
Вычисляем значения исходной функции на концах отрезка и в точках 
:
Следовательно, множеством значений функции на отрезке является отрезок 
.
Сейчас покажем, как находить множество значений непрерывной функции y = f(x) промежутках (a; b) , .
Сначала определяем точки экстремума, экстремумы функции, промежутки возрастания и убывания функции на данном интервале. Далее вычисляем на концах интервала и (или) пределы на бесконечности (то есть, исследуем поведение функции на границах интервала или на бесконечности). Этой информации достаточно, чтобы найти множество значений функции на таких промежутках.
Пример.
Определите множество значений функции на интервале (-2; 2) .
Решение.
Найдем точки экстремума функции, попадающие на промежуток (-2; 2)
:
Точка x = 0
является точкой максимума, так как производная меняет знак с плюса на минус при переходе через нее, а график функции от возрастания переходит к убыванию.
есть соответствующий максимум функции.
Выясним поведение функции при x
стремящемся к -2
справа и при x
стремящемся к 2
слева, то есть, найдем односторонние пределы:
Что мы получили: при изменении аргумента от -2 к нулю значения функции возрастают от минус бесконечности до минус одной четвертой (максимума функции при x = 0 ), при изменении аргумента от нуля к 2 значения функции убывают к минус бесконечности. Таким образом, множество значений функции на интервале (-2; 2) есть .
Пример.
Укажите множество значений функции тангенса y = tgx на интервале .
Решение.
Производная функции тангенса на интервале положительна 
, что указывает на возрастание функции. Исследуем поведение функции на границах интервала:
Таким образом, при изменении аргумента от к значения функции возрастают от минус бесконечности к плюс бесконечности, то есть, множество значений тангенса на этом интервале есть множество всех действительных чисел .
Пример.
Найдите область значений функции натурального логарифма y = lnx .
Решение.
Функция натурального логарифма определена для положительных значений аргумента 
. На этом интервале производная положительна 
, это говорит о возрастании функции на нем. Найдем односторонний предел функции при стремлении аргумента к нулю справа, и предел при x
стремящемся к плюс бесконечности:
Мы видим, что при изменении x от нуля к плюс бесконечности значения функции возрастают от минус бесконечности к плюс бесконечности. Следовательно, областью значений функции натурального логарифма является все множество действительных чисел.
Пример.
Решение.
Эта функция определена для всех действительных значений x
. Определим точки экстремума, а также промежутки возрастания и убывания функции.
Следовательно, функция убывает при , возрастает при , x = 0
- точка максимума, 
соответствующий максимум функции.
Посмотрим на поведение функции на бесконечности:
Таким образом, на бесконечности значения функции асимптотически приближаются к нулю.
Мы выяснили, что при изменении аргумента от минус бесконечности к нулю (точке максимума) значения функции возрастают от нуля до девяти (до максимума функции), а при изменении x от нуля до плюс бесконечности значения функции убывают от девяти до нуля.
Посмотрите на схематический рисунок.
Теперь хорошо видно, что область значений функции есть .
Нахождение множества значений функции y = f(x) на промежутках требует аналогичных исследований. Не будем сейчас подробно останавливаться на этих случаях. В примерах ниже они нам еще встретятся.
Пусть область определения функции y = f(x) представляет собой объединение нескольких промежутков. При нахождении области значений такой функции определяются множества значений на каждом промежутке и берется их объединение.
Пример.
Найдите область значений функции .
Решение.
Знаменатель нашей функции не должен обращаться в ноль, то есть, .
Сначала найдем множество значений функции на открытом луче .
Производная функции 
отрицательна на этом промежутке, то есть, функция убывает на нем.
Получили, что при стремлении аргумента к минус бесконечности значения функции асимптотически приближаются к единице. При изменении x от минус бесконечности до двух значения функции убывают от одного до минус бесконечности, то есть, на рассматриваемом промежутке функция принимает множество значений . Единицу не включаем, так как значения функции не достигают ее, а лишь асимптотически стремятся к ней на минус бесконечности.
Действуем аналогично для открытого луча .
На этом промежутке функция тоже убывает.
Множество значений функции на этом промежутке есть множество .
Таким образом, искомая область значений функции есть объединение множеств и .
Графическая иллюстрация.
Отдельно следует остановиться на периодических функциях. Область значений периодических функций совпадает с множеством значений на промежутке, отвечающем периоду этой функции.
Пример.
Найдите область значений функции синуса y = sinx .
Решение.
Эта функция периодическая с периодом два пи. Возьмем отрезок и определим множество значений на нем.
Отрезку принадлежат две точки экстремума и .
Вычисляем значения функции в этих точках и на границах отрезка, выбираем наименьшее и наибольшее значение:
Следовательно, 
.
Пример.
Найдите область значения функции 
.
Решение.
Мы знаем, что областью значений арккосинуса является отрезок от нуля до пи, то есть, 
или в другой записи . Функция 
может быть получена из arccosx
сдвигом и растяжением вдоль оси абсцисс. Такие преобразования на область значений не влияют, поэтому, 
. Функция 
получается из растяжением втрое вдоль оси Оy
, то есть, 
. И последняя стадия преобразований – это сдвиг на четыре единицы вниз вдоль оси ординат. Это нас приводит к двойному неравенству
Таким образом, искомая область значений есть 
.
Приведем решение еще одного примера, но без пояснений (они не требуются, так как полностью аналогичны).
Пример.
Определите область значений функции 
.
Решение.
Запишем исходную функцию в виде 
. Областью значений степенной функции является промежуток . То есть, . Тогда
Следовательно, 
.
Для полноты картины следует поговорить о нахождении области значений функции, которая не является непрерывной на области определения. В этом случае, область определения разбиваем точками разрыва на промежутки, и находим множества значений на каждом из них. Объединив полученные множества значений, получим область значений исходной функции. Рекомендуем вспомнить 3 слева значения функции стремятся к минус единице, а при стремлении x к 3 справа значения функции стремятся к плюс бесконечности.
Таким образом, область определения функции разбиваем на три промежутка .
На промежутке имеем функцию 
. Так как , то
Таким образом, множество значений исходной функции на промежутке есть [-6;2] .
На полуинтервале имеем постоянную функцию y = -1 . То есть, множество значений исходной функции на промежутке состоит из единственного элемента .
Функция определена для всех действительных значений аргумента. Выясним промежутки возрастания и убывания функции.
Производная обращается в ноль при x=-1
и x=3
. Отметим эти точки на числовой оси и определим знаки производной на полученных интервалах.
Функция убывает на 
, возрастает на [-1; 3]
, x=-1
точка минимума, x=3
точка максимума.
Вычислим соответствующие минимум и максимум функции:
Проверим поведение функции на бесконечности:
Второй предел вычисляли по .
Сделаем схематичный чертеж.
При изменении аргумента от минус бесконечности до -1 значения функции убывают от плюс бесконечности до -2e , при изменении аргумента от -1 до 3 значения функции возрастают от -2e до , при изменении аргумента от 3 до плюс бесконечности значения функции убывают от до нуля, но нуля не достигают.
ГБОУ лицей (экономический) с. Исаклы
Учитель математики Кузаева В.Н.
2016 год
Справочные материалы
Образец решения Найти множество значений функций
Область значения функции 
является
y - любое число
Область значения функции является
y
- любое число
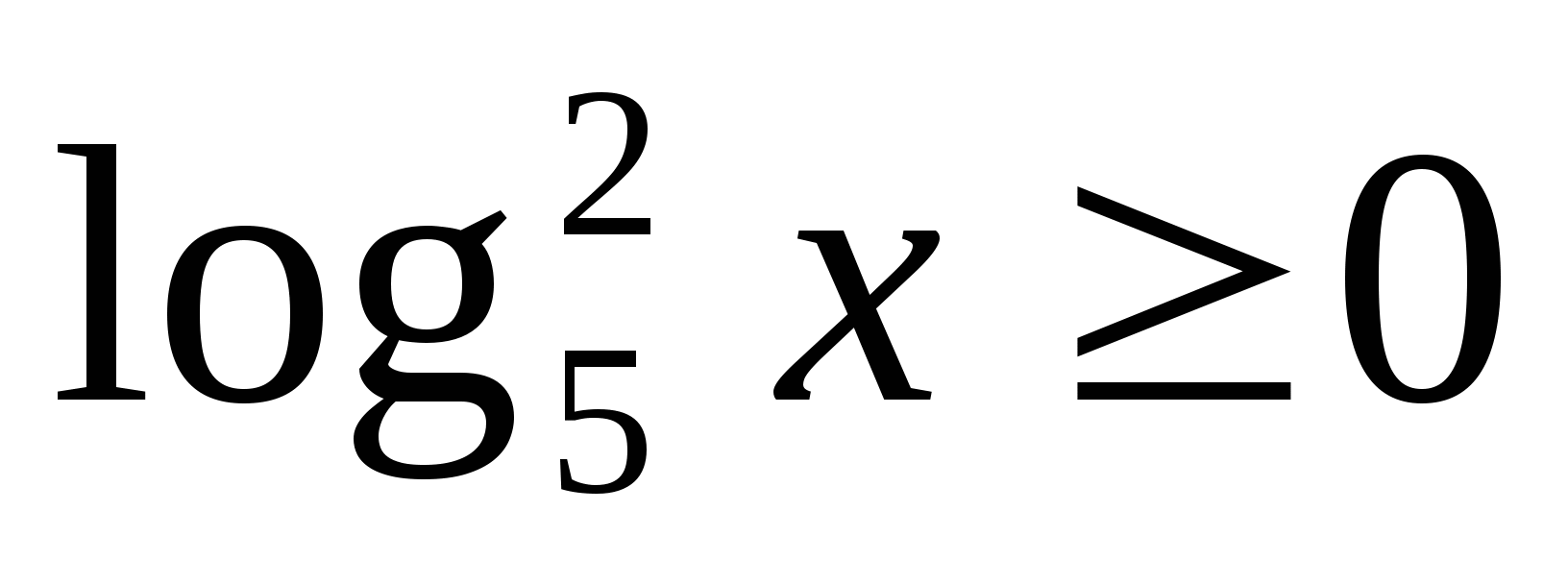
Множество значений
y - любое число
Наибольшее значение
Наименьшее значение
Область определения х
- любое число 
, где 
, где
Множество значений 
y
- любое число
y
- любое число
Шаблоны графиков некоторых тригонометрических функций
Множество значений тригонометрических функций
Вариант 1
У = sin 3х+2.
1) (-5;5) 2) 3) 4) (1;5)
2. Найдите область значения функции у = tg х + 1.
1) 3) (-∞;∞) 4)
1) -6 2) 6 3) -4 4) -2
4. Укажите наименьшее целое число из области значений функции
у = 12,7 + 5 sin (3х-2).
1) -5 2) 8 3) 5 4) 17
5. Укажите функцию, множеством значений которой является отрезок [-2;2].
1) у = cos 2х 2) у = sin 2 x 3) y = cos 2 x +2
4) y = 2 sin 4 x
6. Найдите множество значений функции
y
=
tg
2
x
на отрезке 
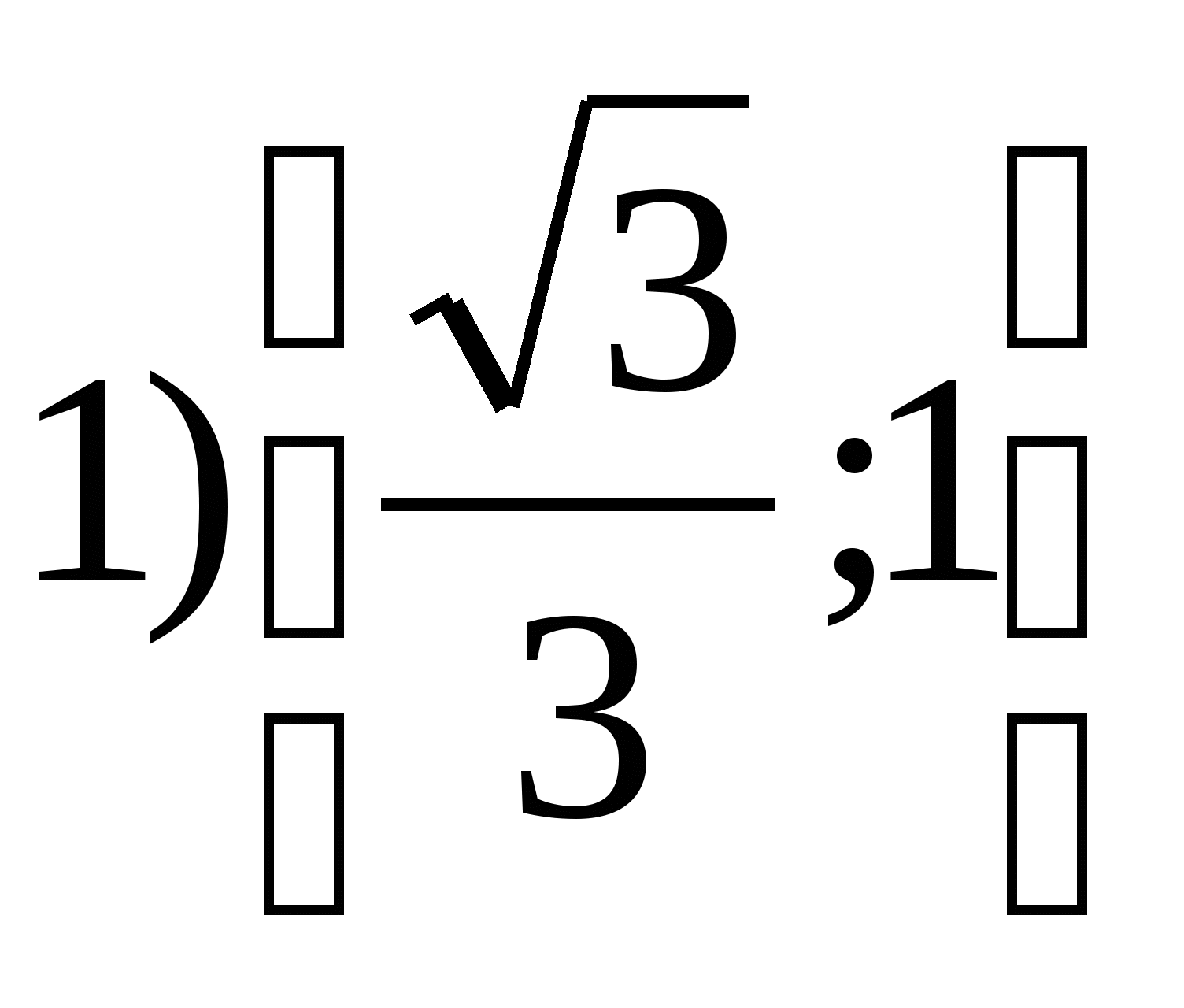
7. Найдите сумму всех целых чисел, которые входят в область значений функции y = 4 cos 2 x – 7.
1) -25 2) 25 3) -22 4) 0
Вариант 2
y = 2 cos 5 x +3.
1) (2;3) 2) 3) (1;5) 4) .
2. Найдите область значения функции 
1) 3) (-∞;∞) 4) .
3. Укажите наименьшее число из области значений функции
1) 4 2) -3 3) 1 4) -7
4. Укажите наибольшее целое из области значений функции
1) 2 2) 13 3) 12 4) -2
5. Укажите функцию, множеством значений которой является отрезок [-5;5].
1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)
4) y = sin 5x + 5
6. Найдите множество значений функции 
на отрезке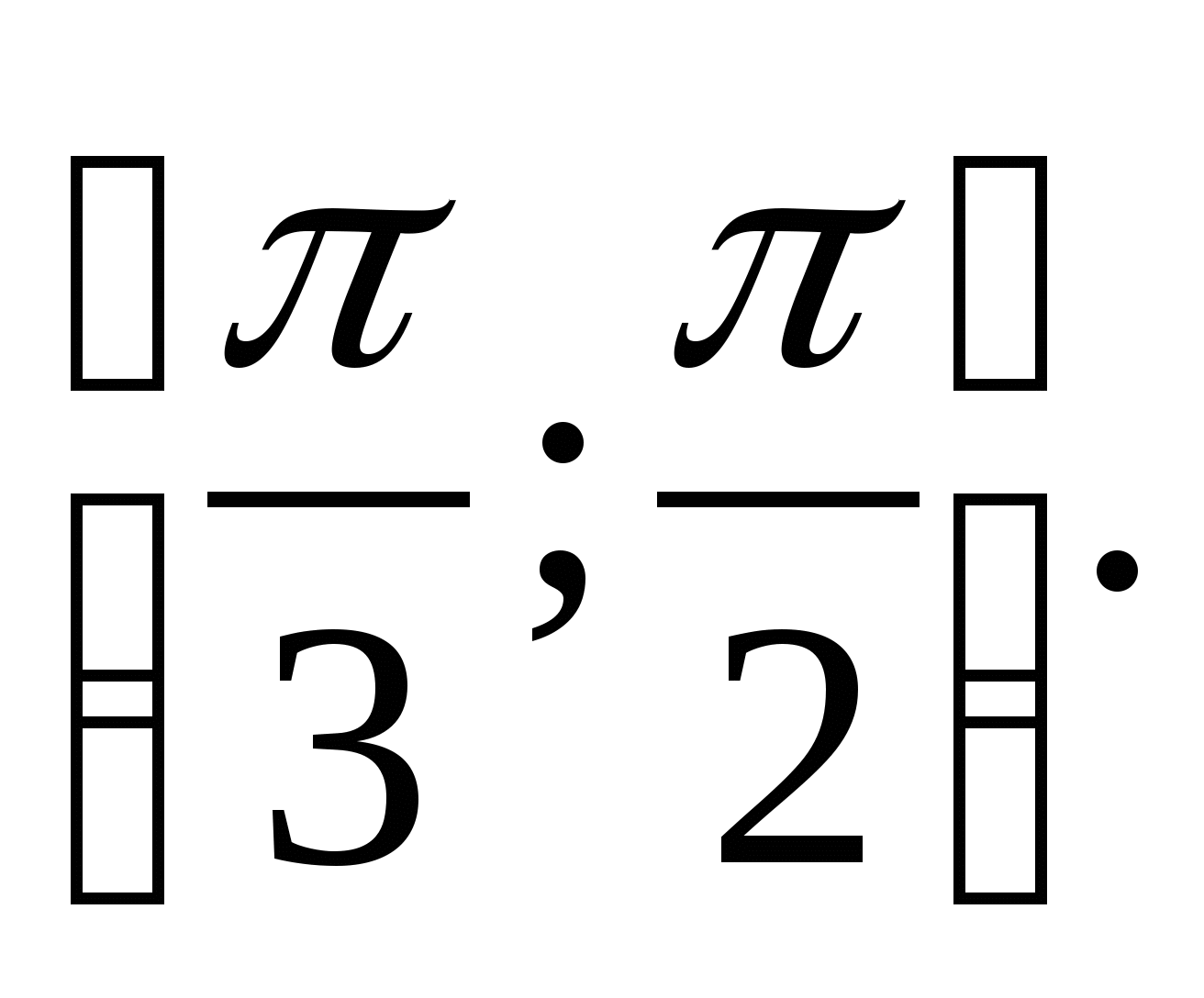 
7. Найдите произведение всех целых чисел, которые входят в область значений функции у = 5 – 3 sin 2 x .
1) 120 2) 14 3) -15 4) 0
Вариант 3
1. Укажите множество значений функции
y
=
sin
3
x
+ 5.
1) (-4;6) 2) 3) [-1;5) 4) (0;6)
1) 2) (0;3) 3) (1;3) 4) [-1;3)
3. Укажите наименьшее число из области значений функции у = 5 tg 2 x +2?
1) 5 2) 0 3) 7 4) 2
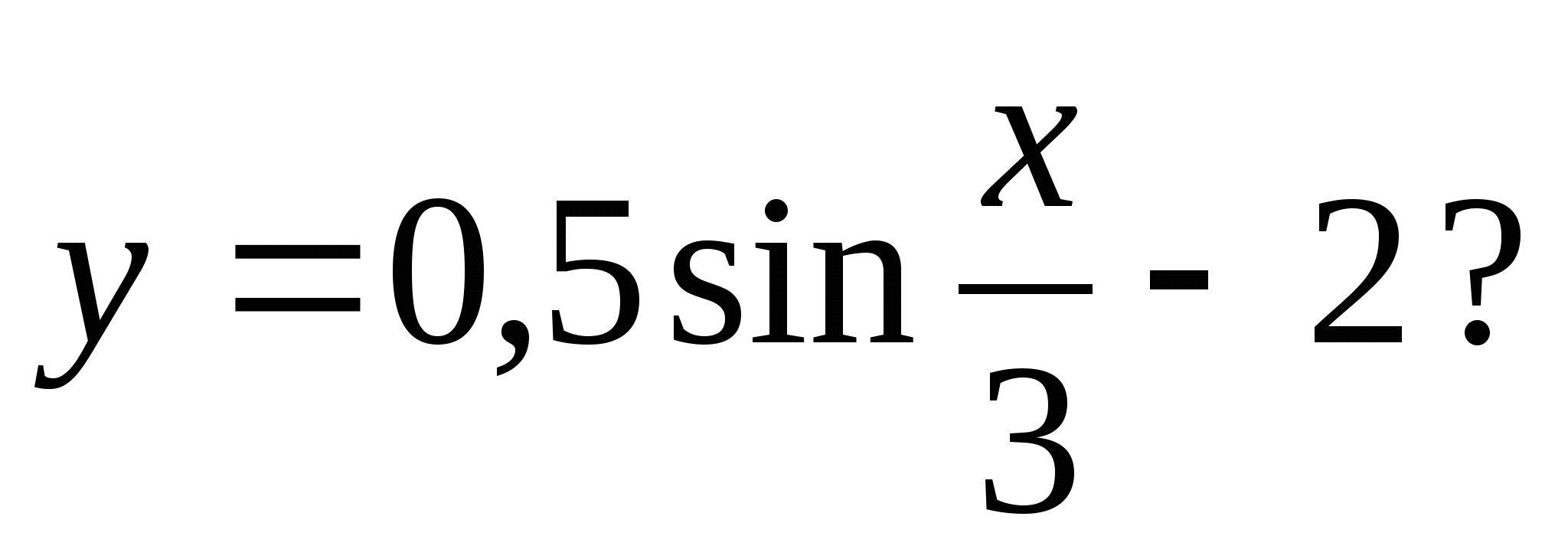
1) -1 2) -2,7 3) -2,3 4)-3
5. Укажите функцию, множеством значений которой является отрезок
[-17;-13].
1) y = 5 sin x – 8 3) y = -cos x +15
2) y = 2 cos x – 15 4) y = 3 sin x +10
6. Укажите наименьшее натуральное число, которое не входит в множество значений функции 
1) 2 2) 4 3) 15 4) 6
7. Сколько целых чисел принадлежит множеству значений функции
y = 2 cos 3 x +10?
1) 2 2) 3 3) 4 5) 5
Вариант 4
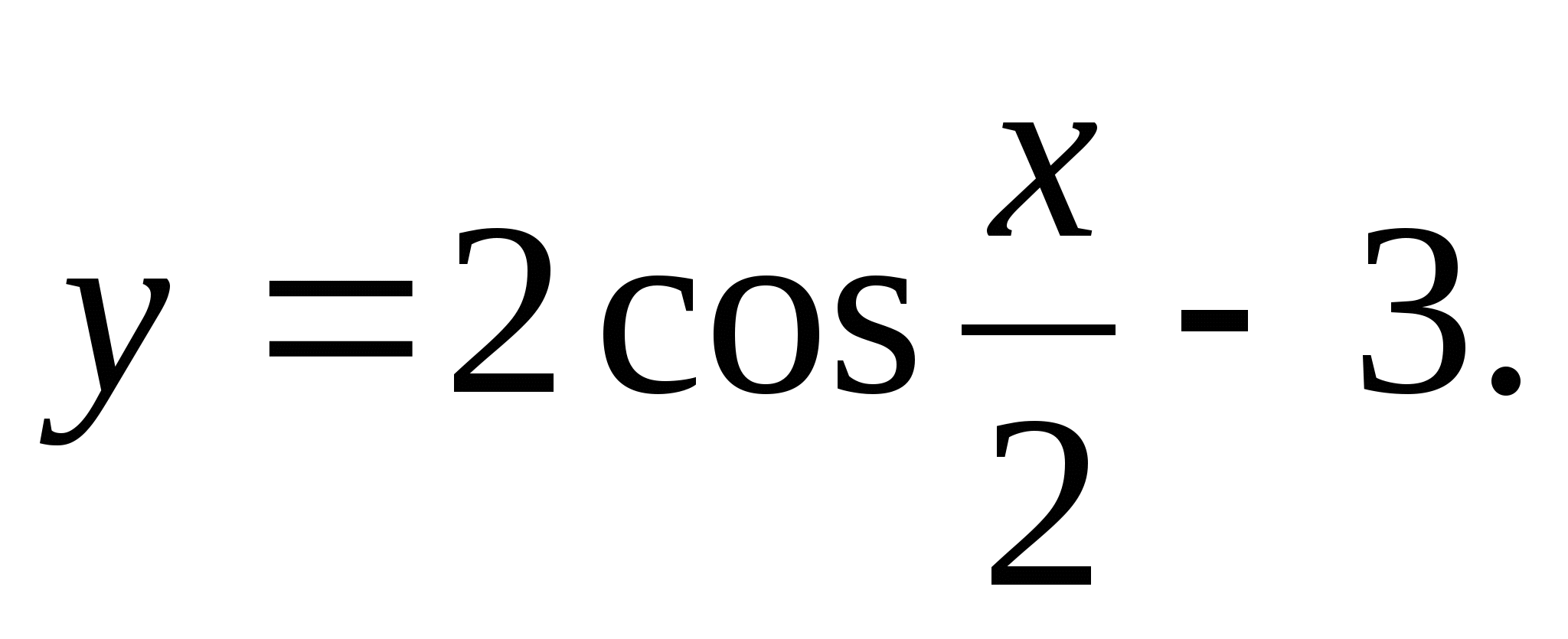
1) 2) 4) (-7;-6)
2. Найдите область значений функции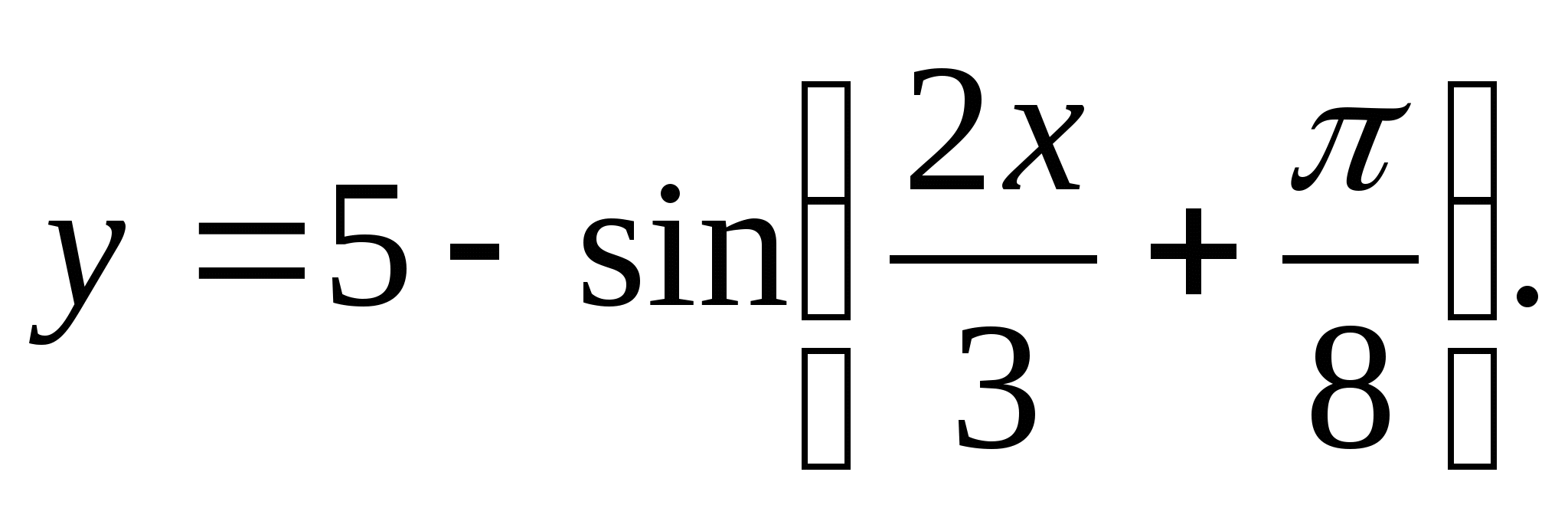 
1) (1;5) 2) 3) (4;6) 4) [-6;-4]
3. Укажите наибольшее число из области значений функции y = -3 ctg 2 x +7.
1) 10 2) 4 3) 7 4) -3
4. Какое из следующих чисел не входит в множество значений функции 
1) -6 2) -5 3) -10 4) -7
5. Укажите функцию, множеством значений которой является отрезок .
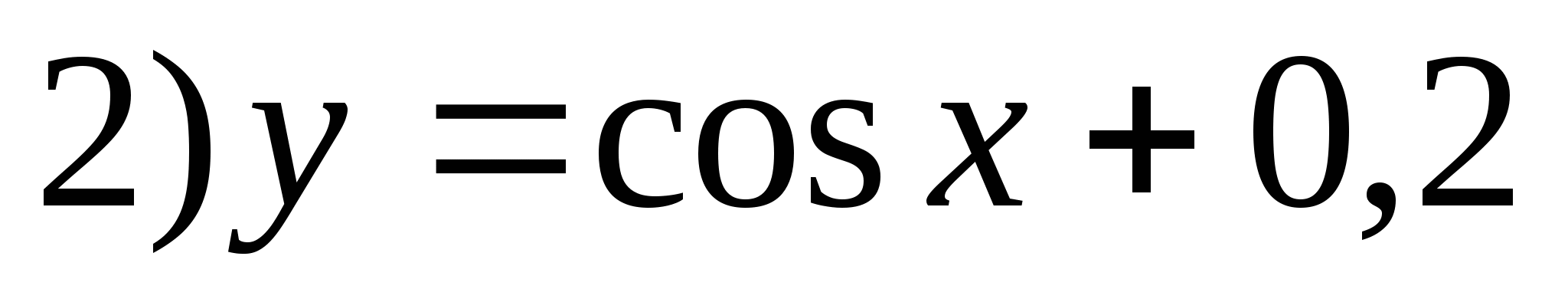
6. Укажите наибольшее целое отрицательное число, которое не входит в область значений функции 
1) -1 2) -25 3) -6 4) -2
7. Сколько целых чисел принадлежит множеству значений функции 
1) 11 2) 3 3) 5 4) 4
Вариант 5
1. Укажите множество значений функции у = 2 - sin 5 x .
1) (2;5) 2) 3) (1;3) 4) [-3;7]
2. Найдите область значений функции 
1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)
3. Укажите наименьшее целое число из области значений функции
y = 3 + sin 2 2 x .
1) 0 2) 1 3) 3 4) 4
4. Какое из следующих чисел входит в множество значений функции 
1) 128 2) 10,5 3) 3 4) -235
5. Укажите функцию, множеством значений которой является отрезок [-9;15].
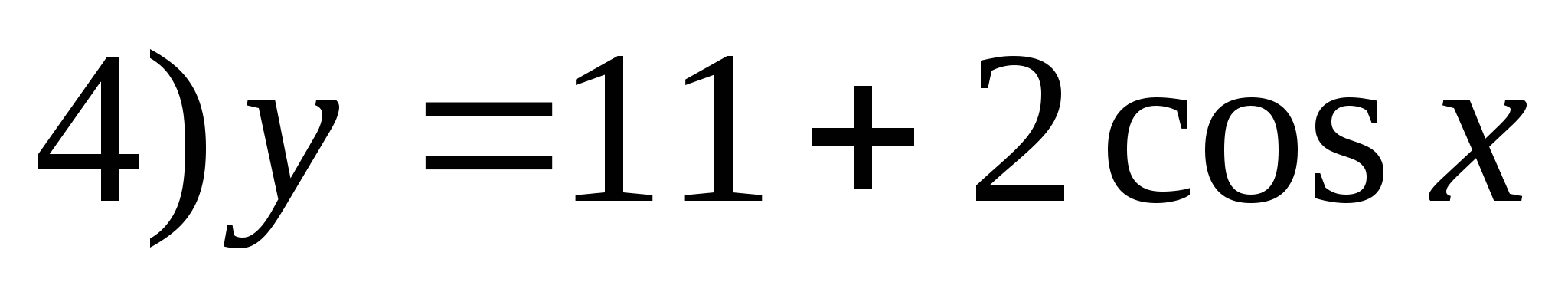
6. Найдите сумму целых чисел, входящих в множество значений функции 
1) 0 2) 7 3) 18 4) 22
7. Найдите наибольшее значение функции 
на отрезке 
1) 0,5 2) 1,5 3) 0 4) 2
Вариант 6
1. Укажите отрезок, соответствующий множеству значений функции 
1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]
2. Найдите область значений функции 
3. Укажите наибольшее число из области значений функции 
1) 5 2) -6 3) -3 4) 4
4. Какое из следующих чисел входит в множество значений функции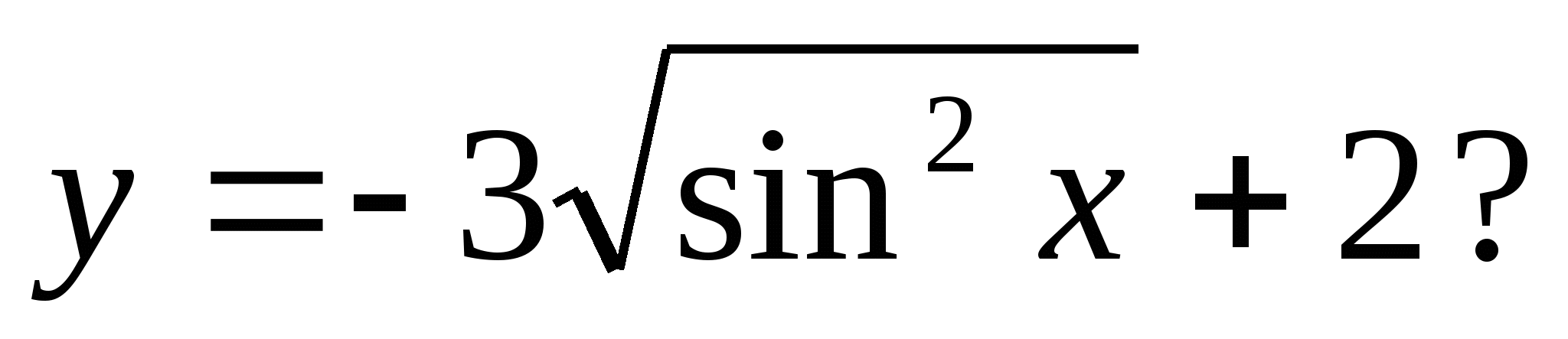 
1) 5 2) 0 3) -3 4) 4
5. Укажите функцию, множество значений которой является отрезок .
1) у = 15 – 7 cos 2x 3) y = 7 cos 2x + 3
2) y = 5 cos 4 x 4) y = - tg 2 x + 1
6. Найдите произведение целых чисел, входящих в множество значений
y = 3,8 – 1,4 sin 3 x .
1) 17 2) 12 3) 0 4) 60
7. Найдите множество значений функции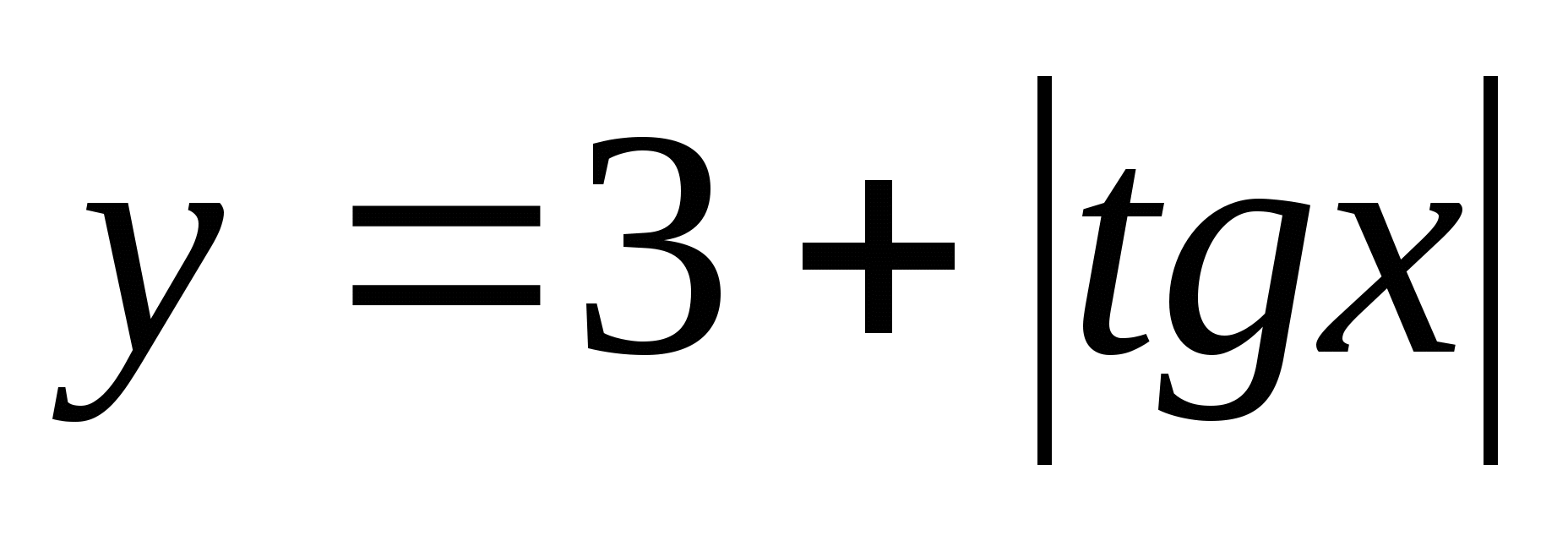 
на промежутке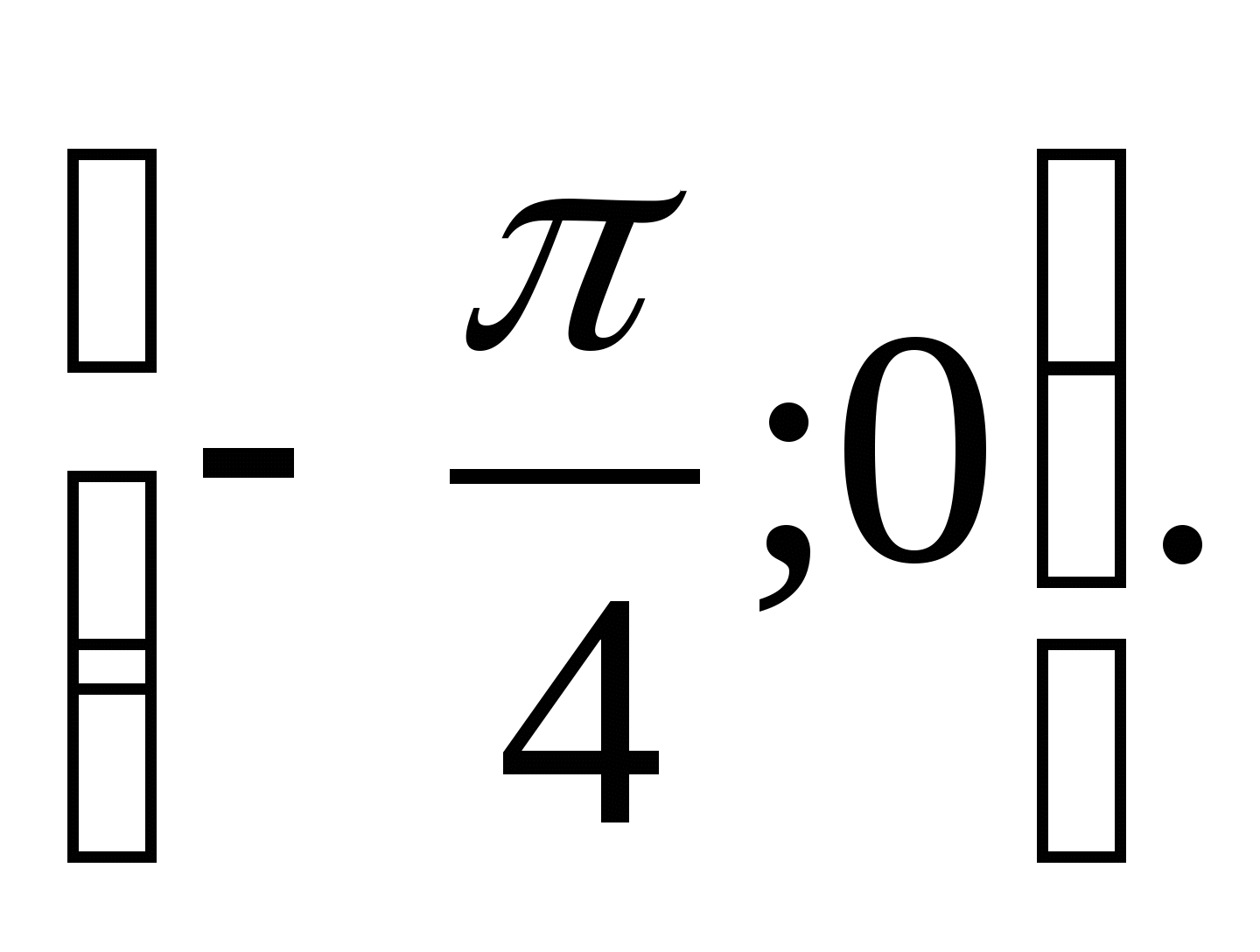 
1) (3;4) 2) 3)
Вариант 7
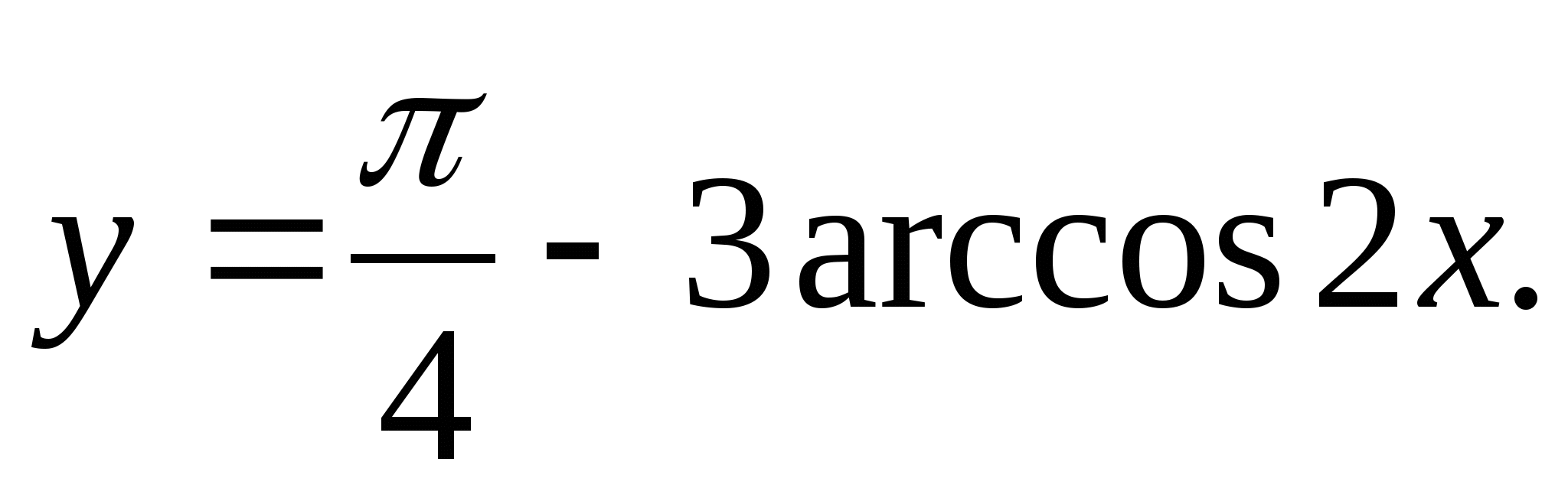
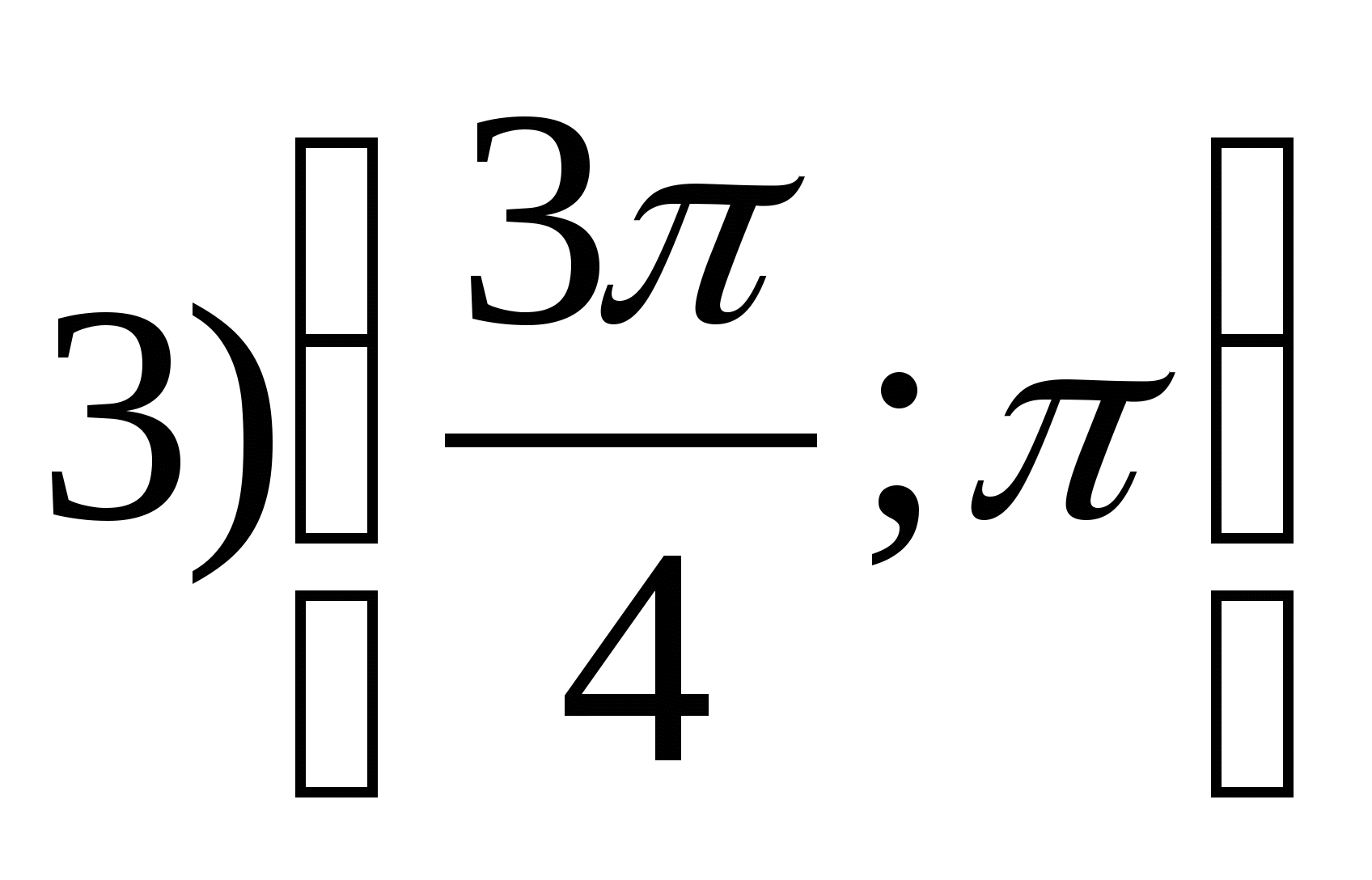
2. Найдите наименьшее целое значение функции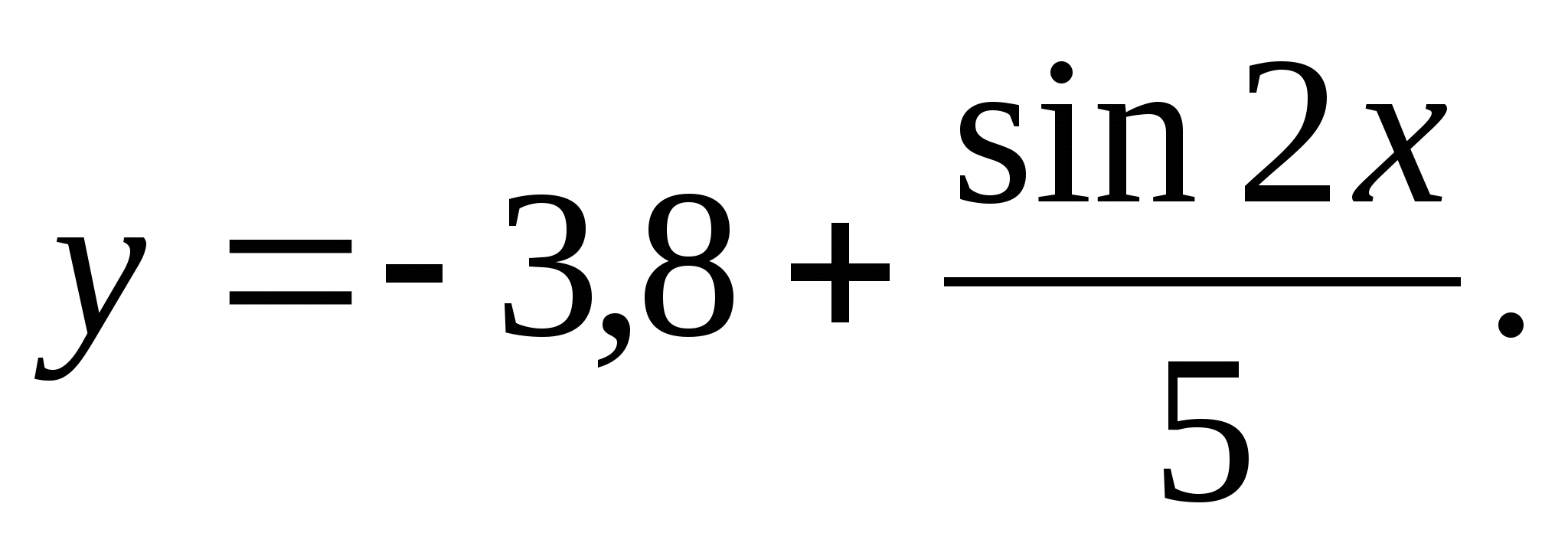 
1) 2 2) 0 3) -3 4) -4
1) 0 2) 2 3) 4 4) 6
4. При каких значениях а уравнение sin (3 x -4)+5= a разрешимо?
1) 2) 3) (4;6) 4) (-6;4]
sin 2 2 x – 2.
1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]
на промежутке 
2) 0 3) 1
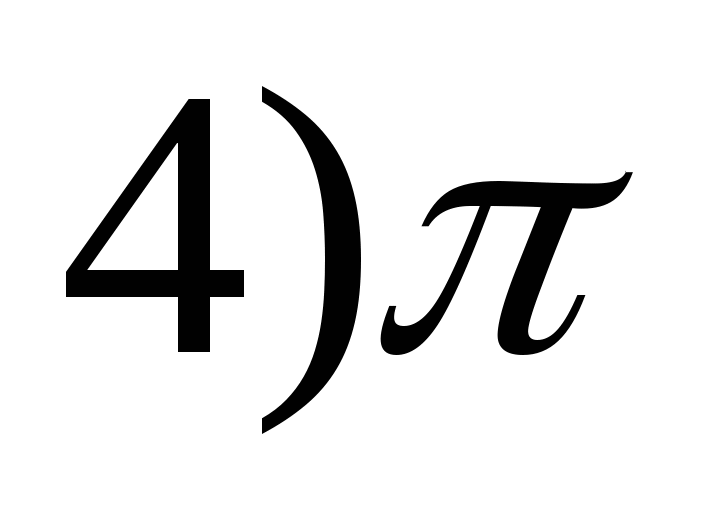
y = 4 sin (x 4 ) -2?
1) 8 2) 9 3) 7 4) 10
Вариант 8
1. Найдите множество значений функции y = arctg x - 2π.
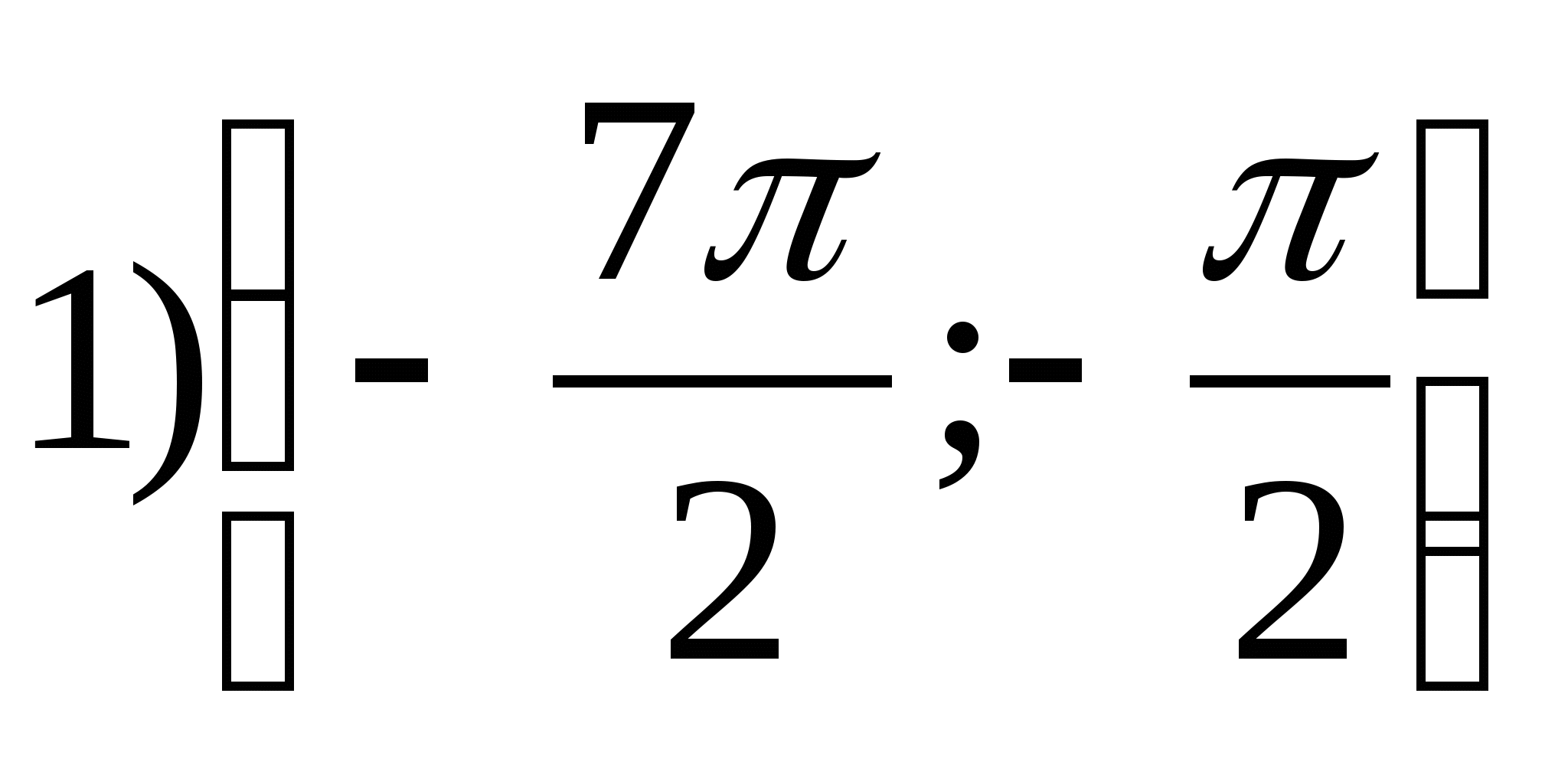
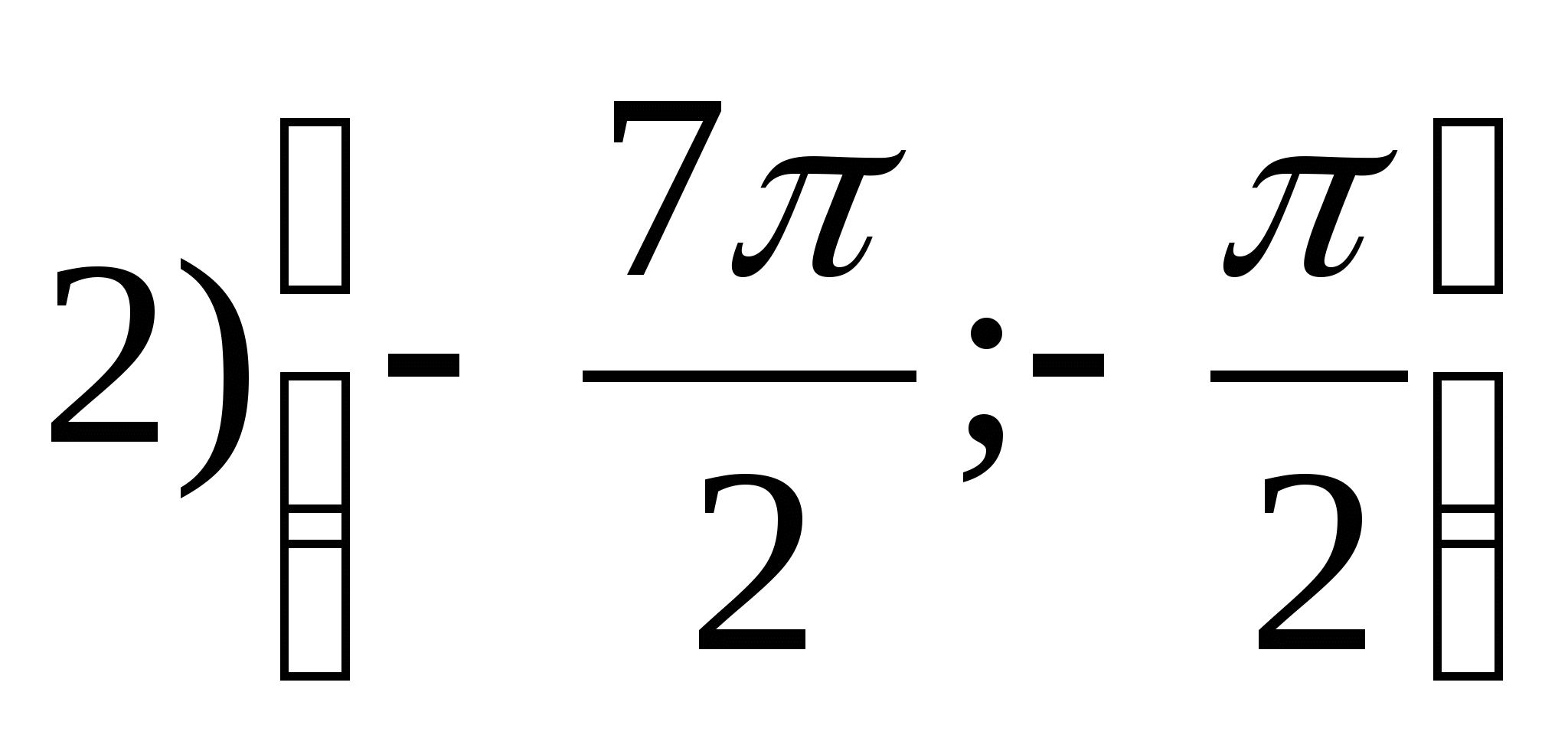
2. Найдите наибольшее значение функции 
1) 1,75 2) 0 3) 2,25 4) -1,75
3. Какое из следующих чисел может быть значением функции 
1) -4 2) -2 3) 0 4) 2
4. При каких значениях р уравнение -2+ cos (4 x -1)= p имеет корни?
1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)
5. Найдите множество значений функции y = -2 tg 2 x + 1.
1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)
на промежутке 
.
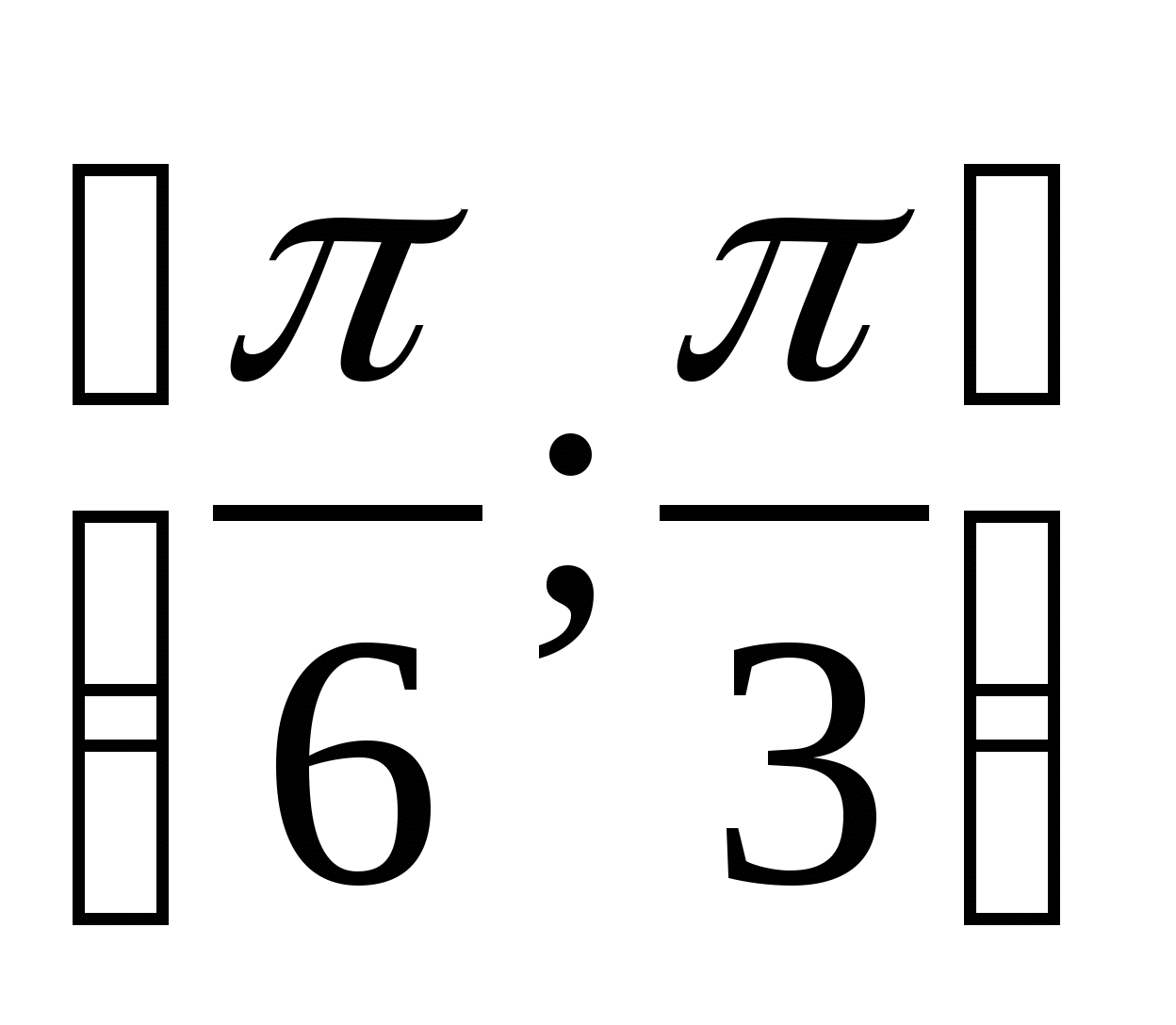1) 0 2) 1 3) -1 4) 3
7. Сколько целых чисел принадлежит области значений функции
1) 4 2) 3 3) 5 4) 2
Вариант 9
1. Найдите область значений функции 
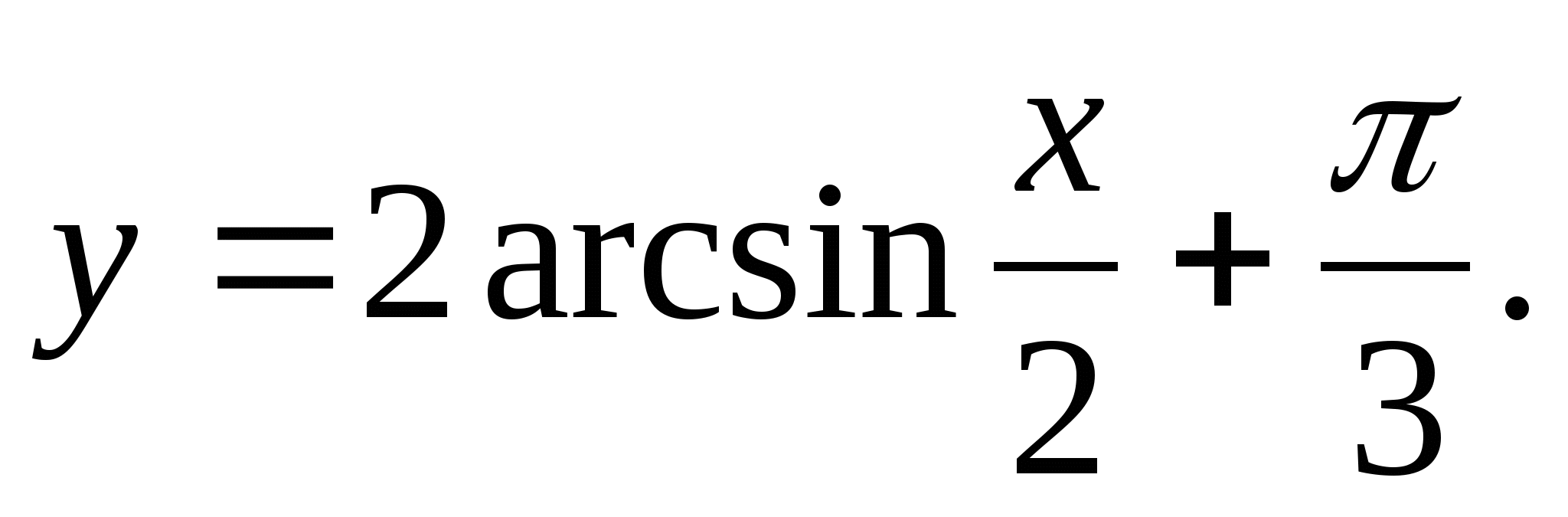
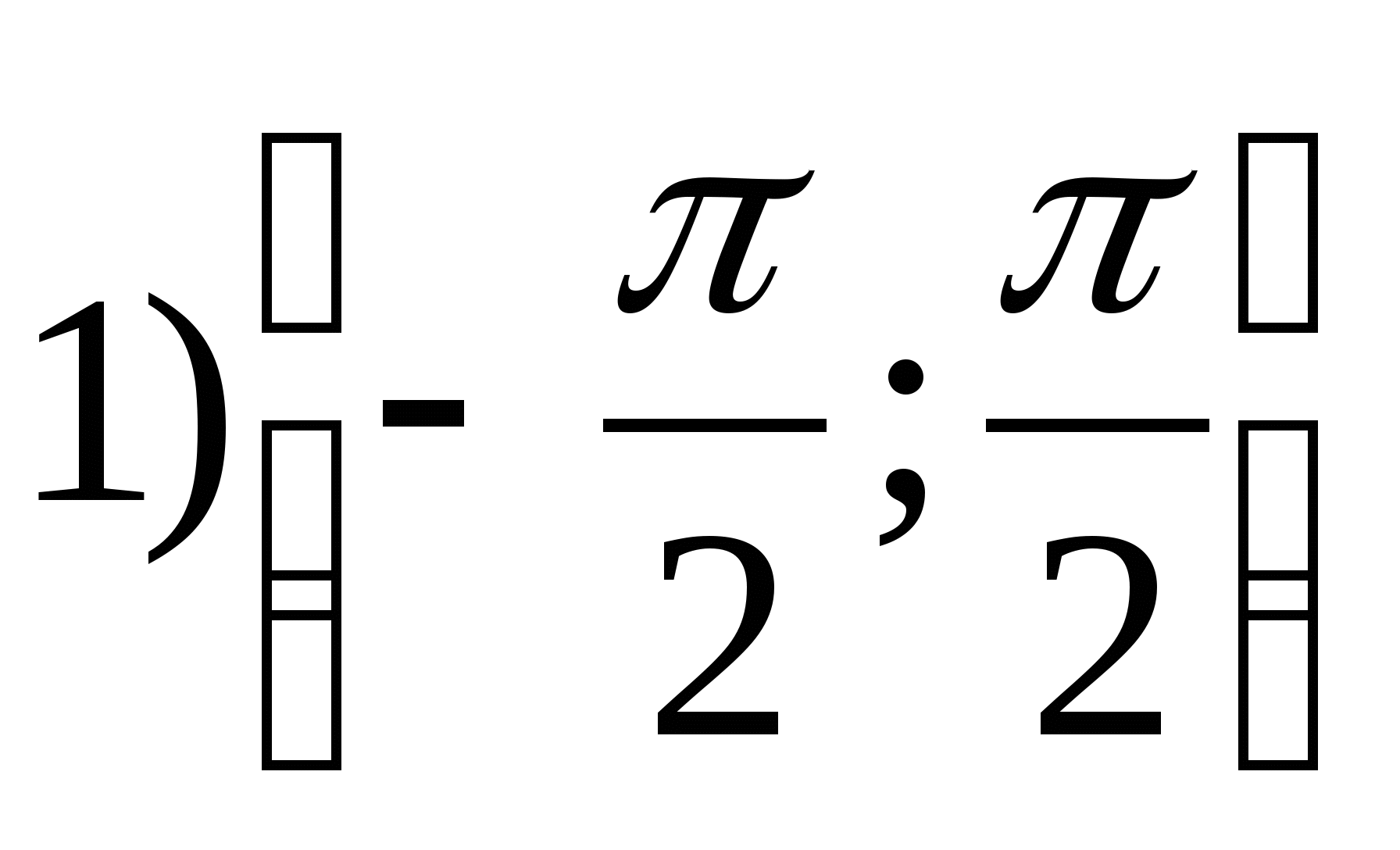
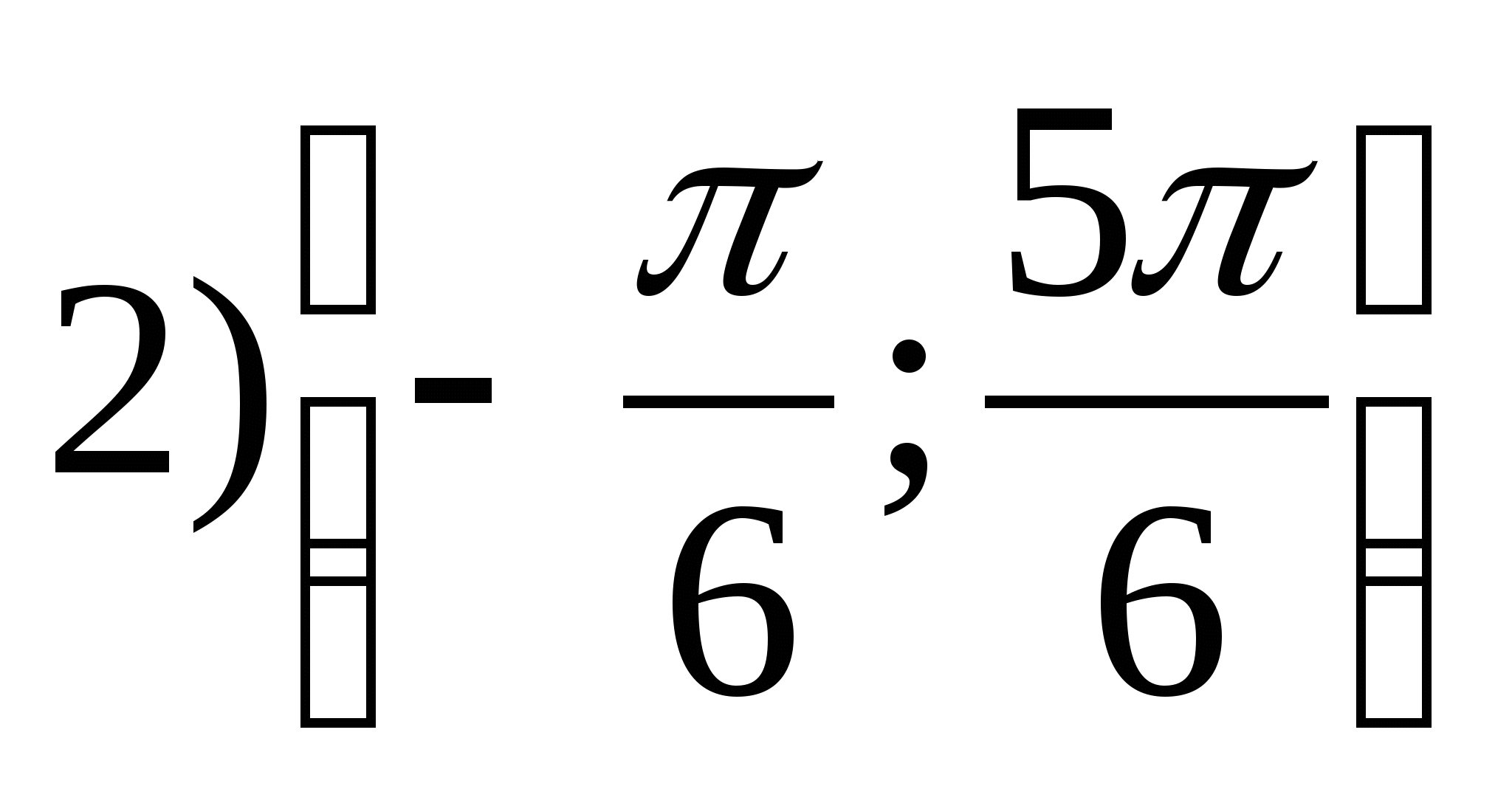
2. Найдите наибольшее целое значение функции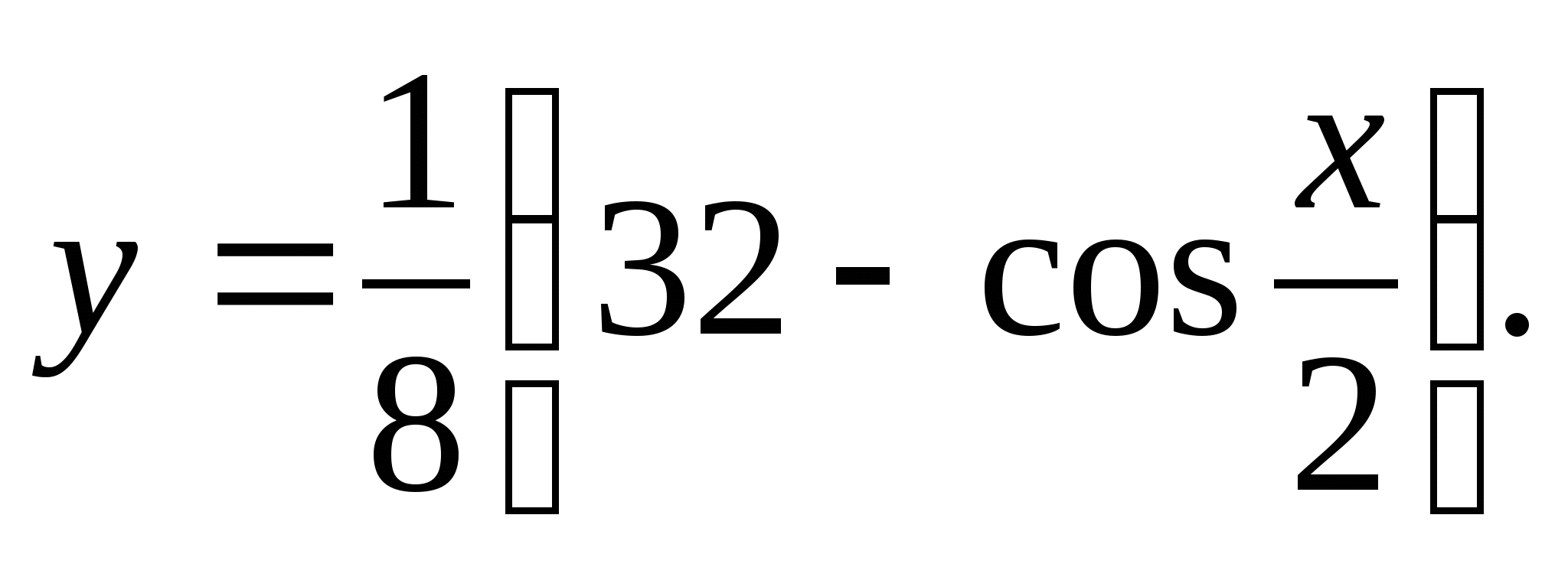 
1) 4 2) 5 3) 6 4) 7
3. Какое из следующих чисел может быть значением функции 
1) 0 2) 3 3) 6 4) 9
k уравнение – k + sin (2 x -1) = 2 разрешимо?
1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]
5. Найдите множество значений функции у = - cos 2 3 x + 4.
1) 2) 3) 4)
6. Укажите наименьшее значение функции на промежутке 
2) -1 3) 0 4) 1
7. Найдите, сколько целых чисел входит в область значений функции у = 12 cos 3 x +5 sin 3 x .
1) 13 2) 27 3) 26 4) 14
Вариант 10
1. Найдите область значений функции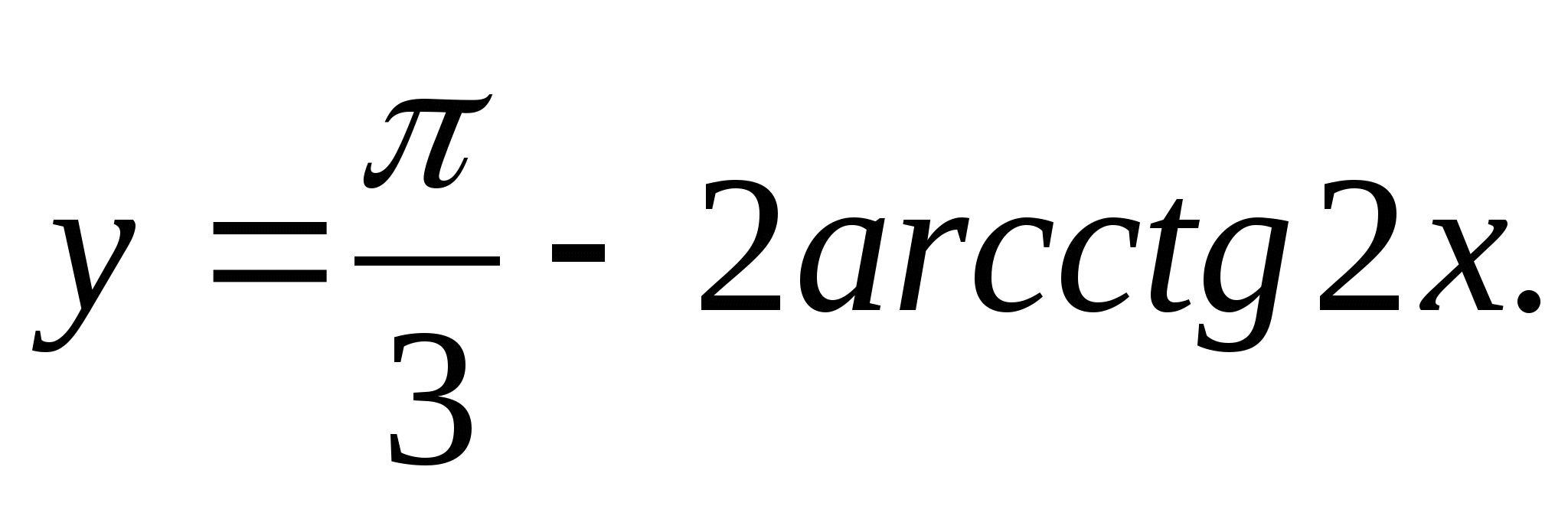 
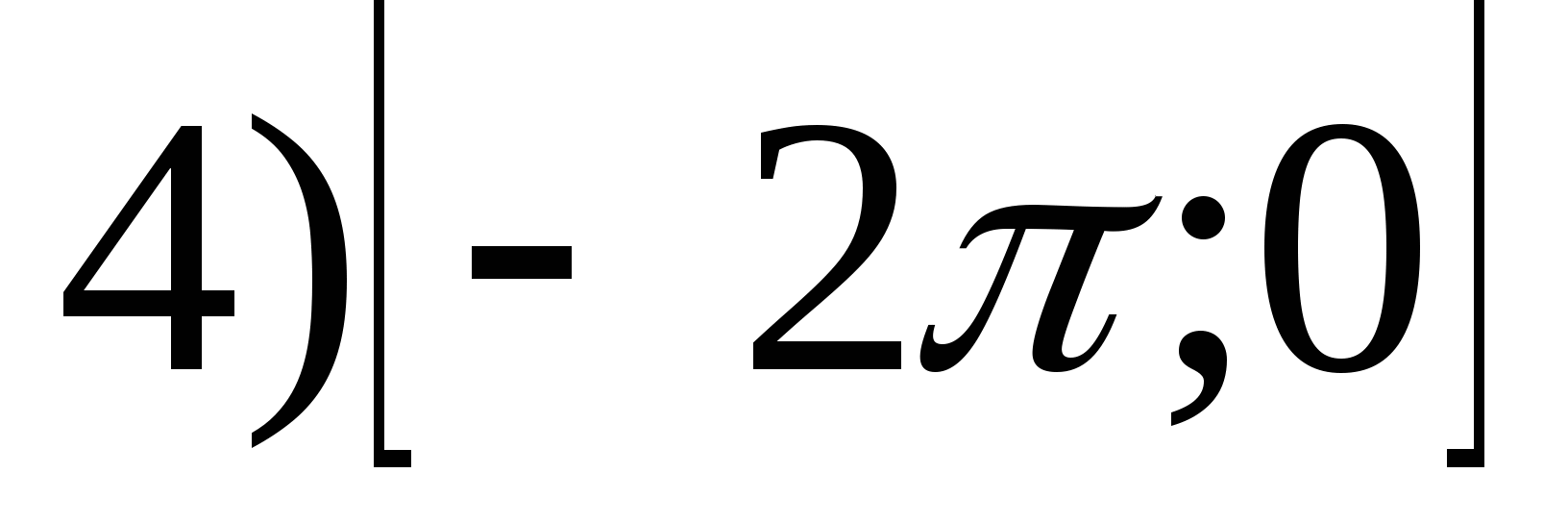
2. Найдите наименьшее значение функции 
1) 3,5 2) 0 3) 2,5 4) -3,5
3. Какое из следующих чисел может быть значением функции 
1) -4 2) -1 3) 3 4) 7
4. При каких значениях параметра m уравнение cos (3 x + 2)- m = 5 имеет корни?
1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]
5. Найдите множество значений функции у = -2 ctg 2 3 x + 7.
1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]
6. Укажите наибольшее значение функции 
на промежутке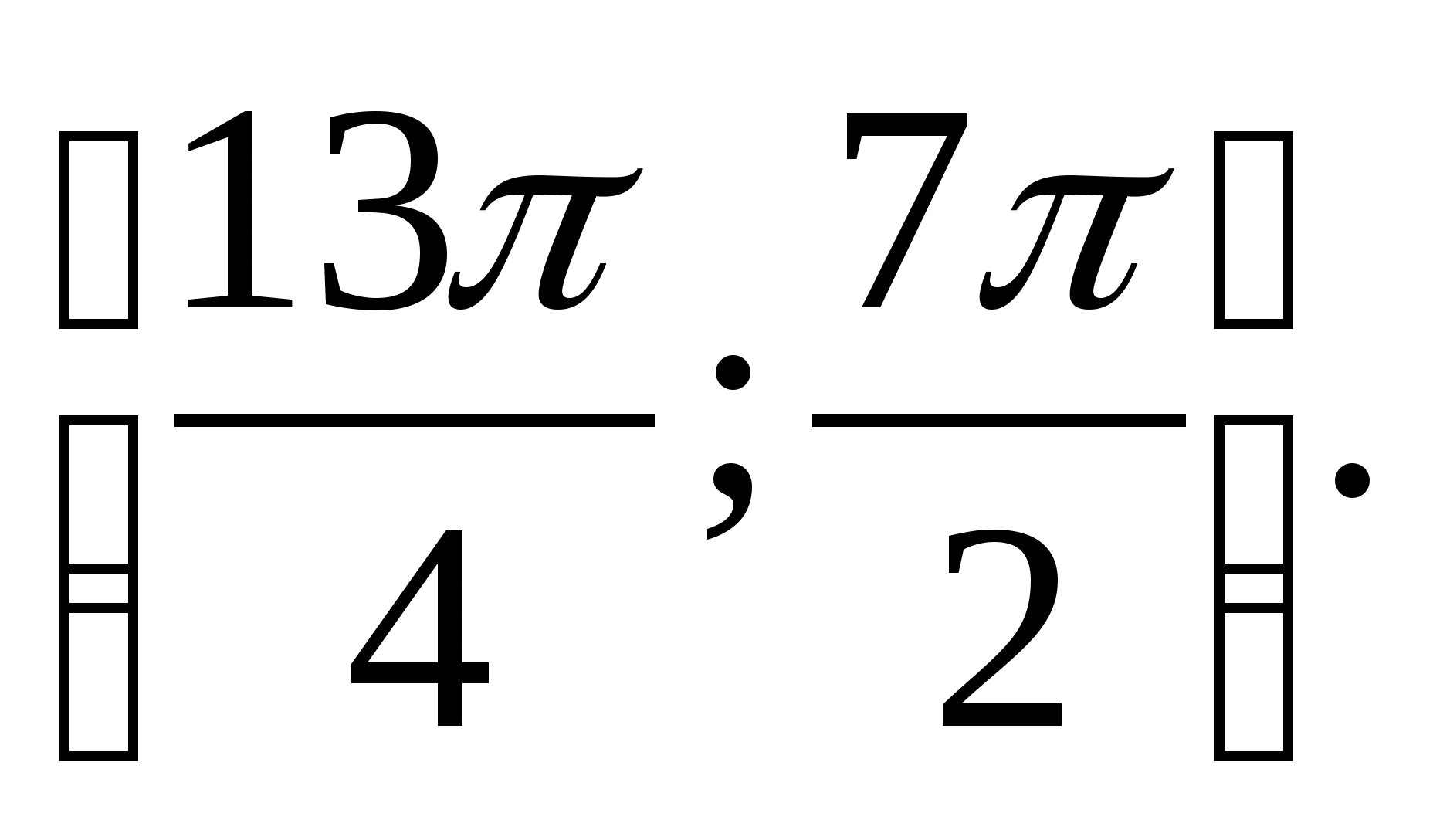 
2) 0 3) 2 4) 1
7. Найдите, сколько целых чисел входит в область значений функции 
1) 30 2) 35 3) 17 4) 7
Множество значений показательной и логарифмической функций
Вариант 1
1. Найдите область значений функции 
1) 4) (-∞;3)
2. Укажите множество значений функции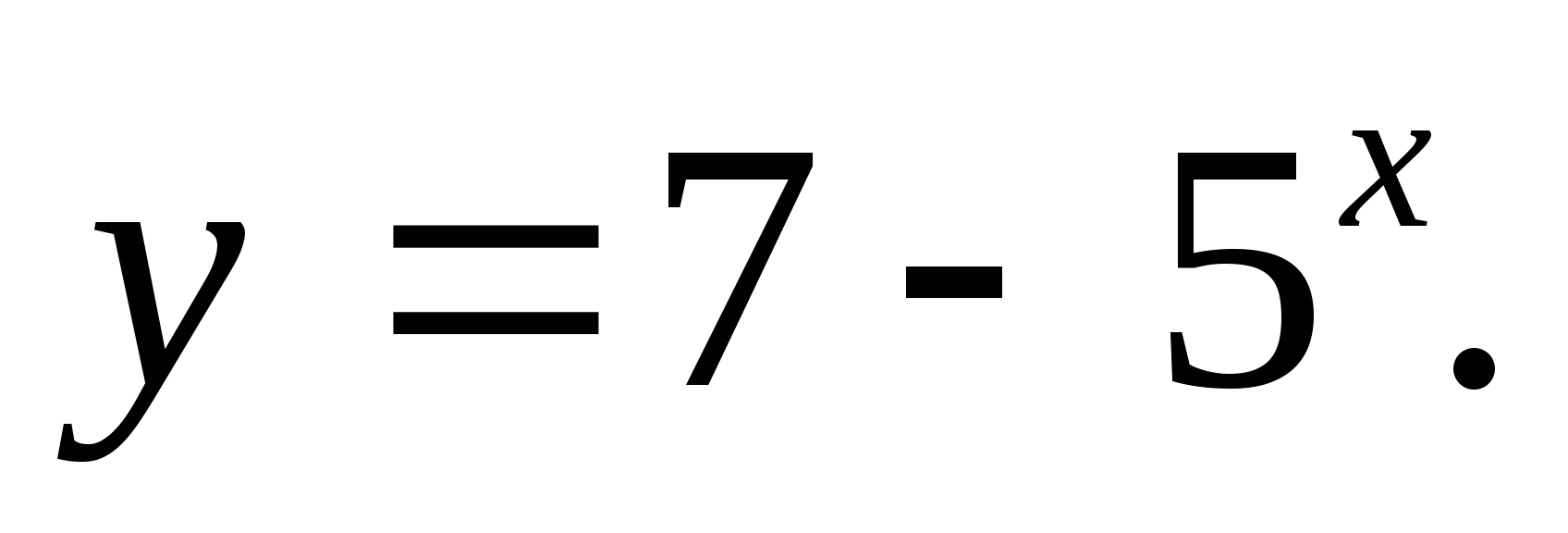 
1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]
1) 0 2) 4 3) -3 4) -4
1) 15 2) 20 3) 43 4) 28
1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)
6. Укажите наименьшее целое значение функции 
1) 1 2) -1 3) 0 4) -5
7. Укажите функцию, множеством значений которой является промежуток (1;∞).
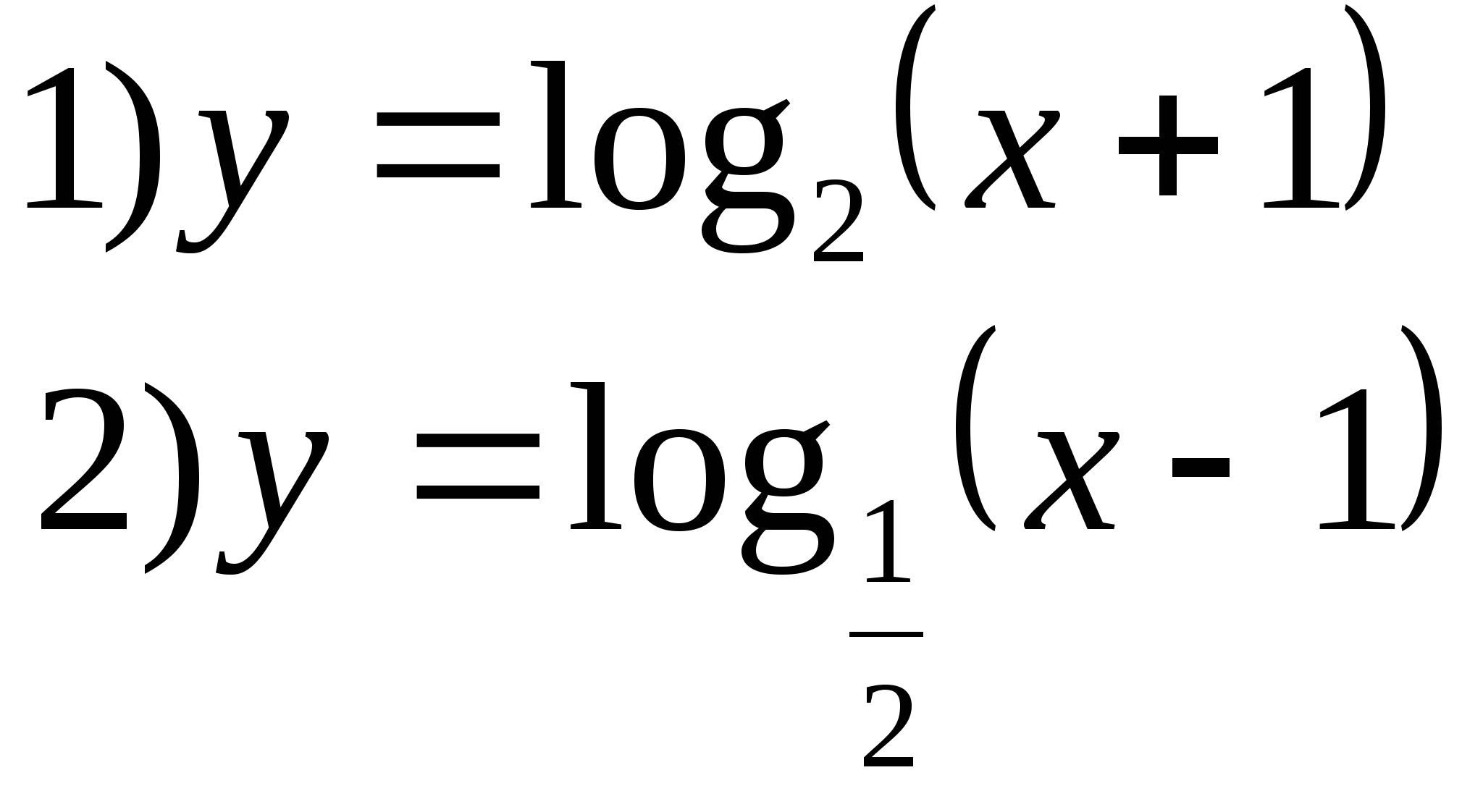
Вариант 2
1. Укажите множество значений функции 
1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)
2. Найдите область значений функции 
1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)
3. Укажите наименьшее целое значение функции 
1) -12 2) -11 3) -10 4) -15
4. Укажите число, не принадлежащее множеству значений фунукции 
1) -42 2) 3 3) 1 4) -20
5. Укажите множество значений функции 
1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]
6. Укажите наибольшее целое значение функции 
1) 10 2) 3 3) 9 4) 2
7. Укажите функцию, множеством значений которой является промежуток
(-∞;13).
Вариант 5
1. Укажите наименьшее целое значение функции 
1) 0 2) -1 3) -2 4) -3
2. Какое из следующих чисел входит в область значений функции 
1) -3 2) -4 3) 5 4) 0
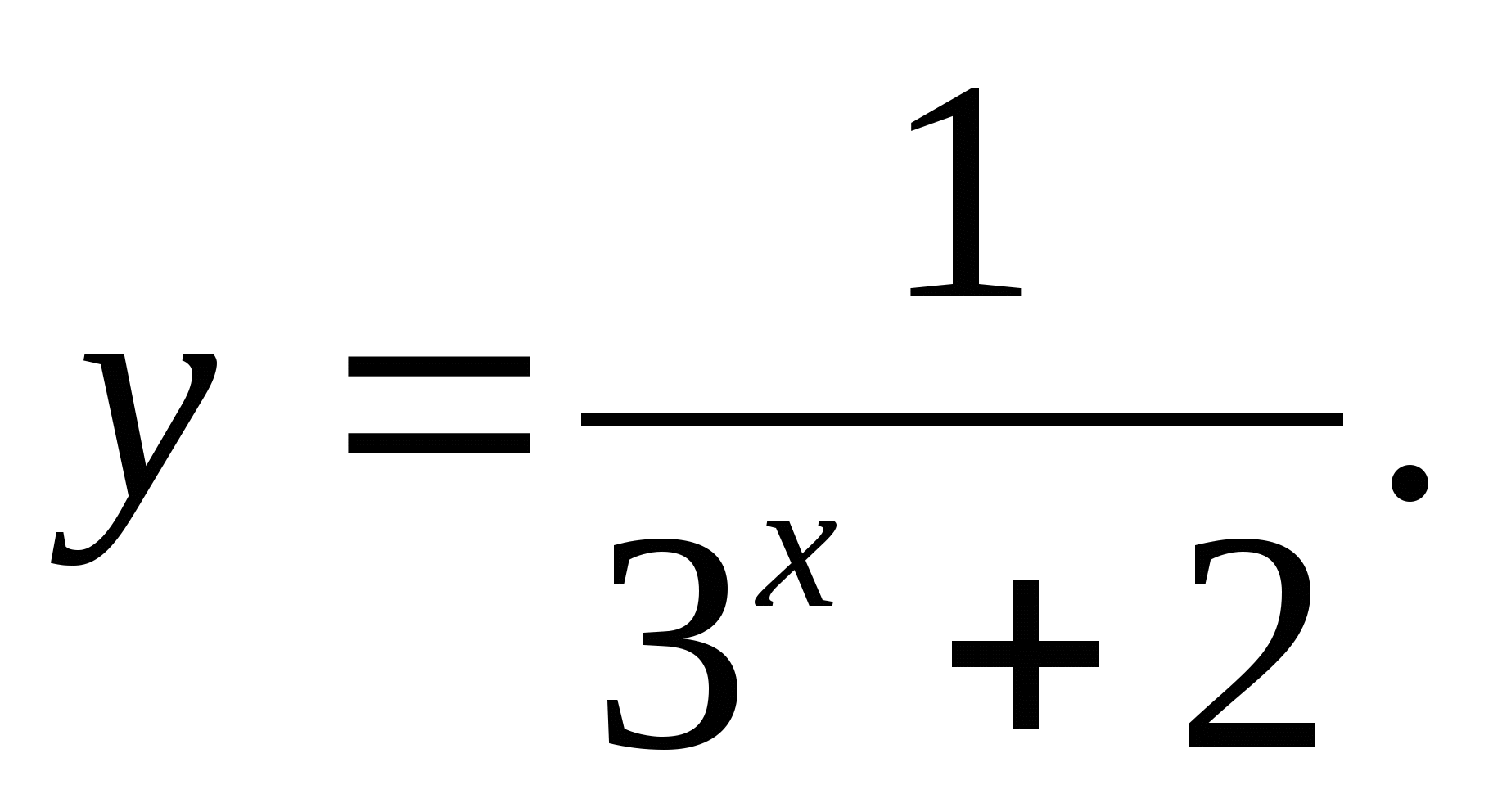
1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)
6. Найдите, на каком отрезке функция 
принимает наибольшее значение, равное 2, и наименьшее значение, равное -3.
1) 2) (-5;2) 3) 4) (-3;2)
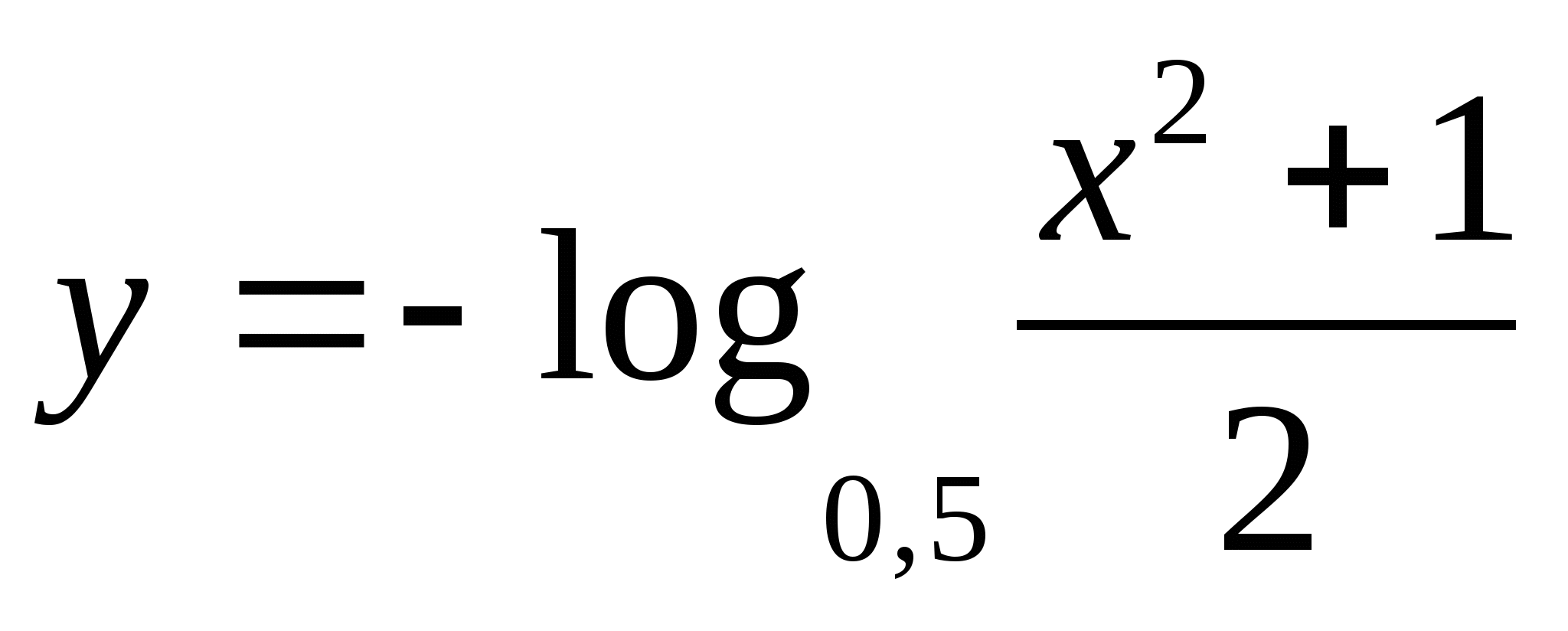на промежутке 
1) -1/2 2) 5 3) 2 4) 4
8. Найдите сумму всех натуральных чисел, не входящих в множеств значений функции 
1) 3 2) 6 3) 10 4) 8
Вариант 6
1. Укажите наибольшее целое значение функции 
1) 2 2) 4 3) 3 4) 5
2. Какое из следующих чисел не входит в область значений функции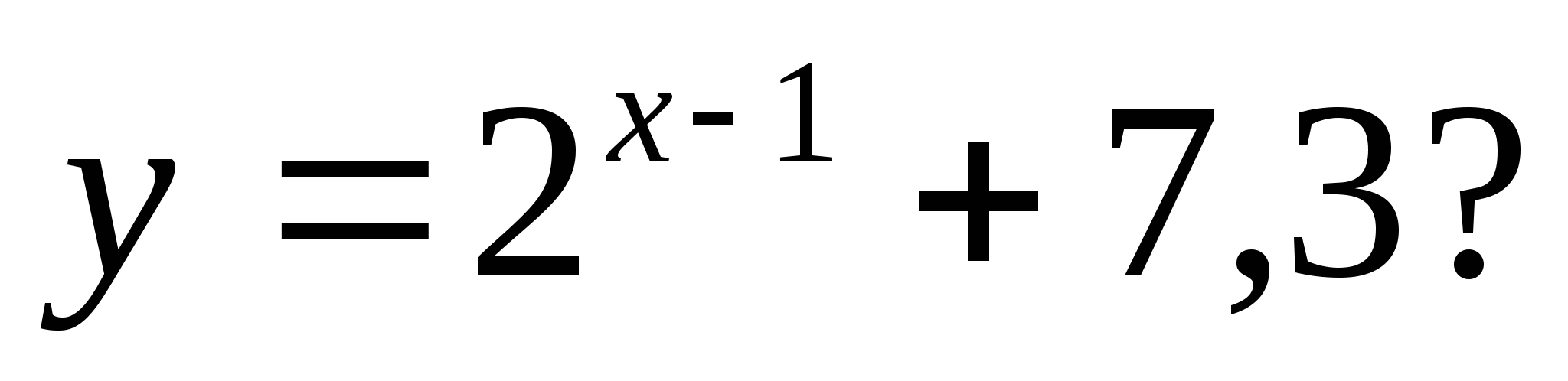 
1) 35 2) 7, 28 3) 7, 85 4) 128
3. Укажите множество значений функции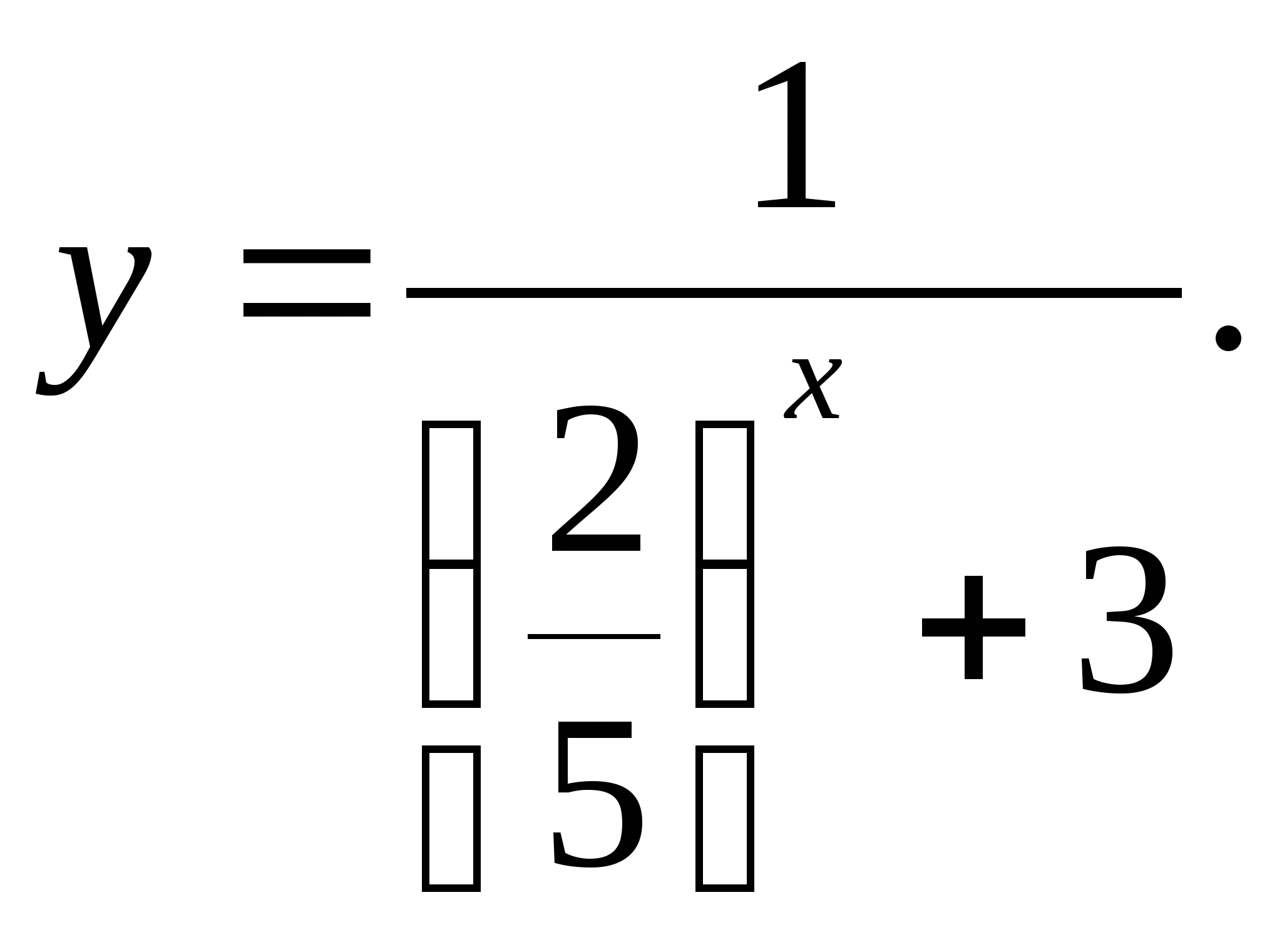 
1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)
4. Найдите все точки на ОУ, являющиеся проекциями точек графика функции 
1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)
6. Найдите на каком отрезке функция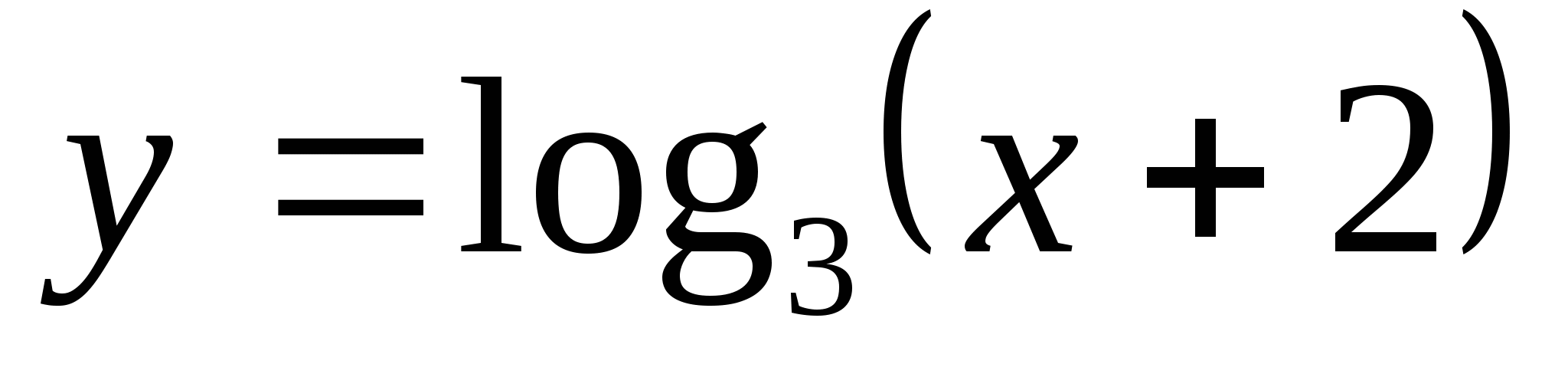 
принимает наименьшее значение, равное -2, и наибольшее значение, равное 4.
1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)
7. Укажите наибольшее значение функции 
на промежутке
[-0,9; 0]. 2. Найдите наименьшее значение функции на отрезке .
4. Сколько целых значений принимает функция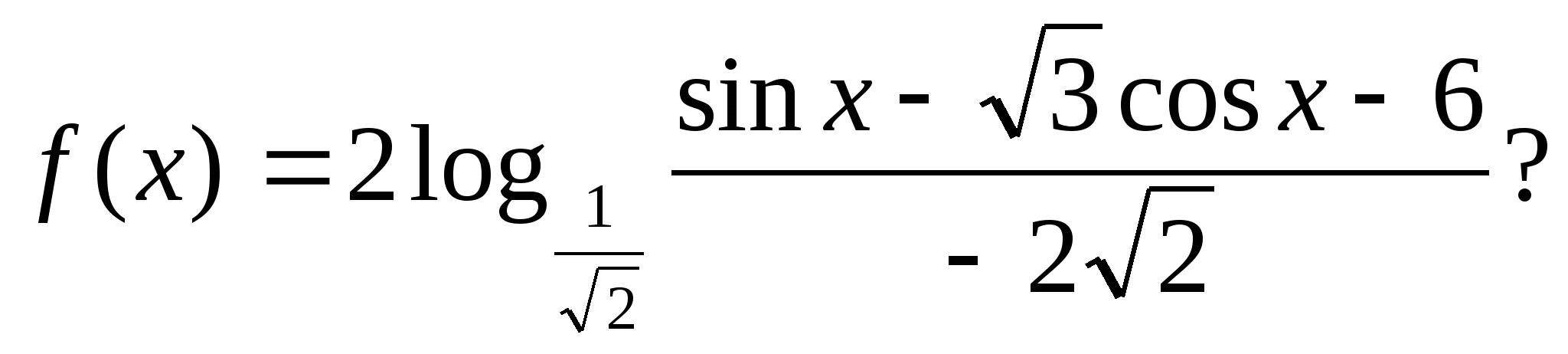 
Ответы
Часть 1
Множество значений показательной и логарифмической функции
Часть 2
Понятие функции и всё, что с ним связано, относится к традиционно сложным, не
до конца понятым. Особым камнем преткновения при изучении функции и подготовке к
ЕГЭ являются область определения и область значений (изменения) функции.
Нередко учащиеся не видят разницы между областью определения функции и областью
её значений.
И если задачи на нахождение области определения функции учащимся удаётся
освоить, то задачи на нахождение множества значений функции вызывают у них
немалые затруднения.
Цель данной статьи: ознакомление с методами нахождения значений функции.
В результате рассмотрения данной темы был изучен теоретический материал,
рассмотрены способы решения задач на нахождение множеств значений функции,
подобран дидактический материал для самостоятельной работы учащихся.
Данная статья может быть использована учителем при подготовке учащихся к
выпускным и вступительным экзаменам, при изучении темы “Область значения
функции” на факультативных занятиях элективных курсах по математике.
I. Определение области значений функции.
Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y 0 , для каждого из которых найдётся такое число x 0 , что: f(x 0) = y 0 .
Напомним области значений основных элементарных функций.
Рассмотрим таблицу.
| Функция | Множество значений |
| y = kx+ b | E(y) = (-∞;+∞) |
| y = x 2n | E(y) = |
| y = cos x | E(y) = [-1;1] |
| y = tg x | E(y) = (-∞;+∞) |
| y = ctg x | E(y) = (-∞;+∞) |
| y = arcsin x | E(y) = [-π/2 ; π/2] |
| y = arcos x | E(y) = |
| y = arctg x | E(y) = (-π/2 ; π/2) |
| y = arcctg x | E(y) = (0; π) |
Заметим также, что областью значения всякого многочлена чётной степени является промежуток , где n – наибольшее значение этого многочлена.
II. Свойства функций, используемые при нахождении области значений функции
Для успешного нахождения множества значений функции надо хорошо знать свойства основных элементарных функций, особенно их области определения, области значений и характер монотонности. Приведём свойства непрерывных, монотонных дифференцируемых функций, наиболее часто используемые при нахождении множества значений функций.
Свойства 2 и 3, как правило, используются вместе свойством элементарной функции быть непрерывной в своей области определения. При этом наиболее простое и краткое решение задачи на нахождение множества значений функции достигается на основании свойства 1, если несложными методами удаётся определить монотонность функции. Решение задачи ещё упрощается, если функция, вдобавок, – чётная или нечётная, периодическая и т.д. Таким образом, при решении задач на нахождение множеств значений функции следует по мере надобности проверять и использовать следующие свойства функции:
- непрерывность;
- монотонность;
- дифференцируемость;
- чётность, нечётность, периодичность и т.д.
Несложные задачи на нахождение множества значений функции в большинстве своём ориентированны:
а) на использование простейших оценок и ограничений: (2 х >0, -1≤sinx?1, 0≤cos 2 x?1 и т.д.);
б) на выделение полного квадрата: х 2 – 4х + 7 = (х – 2) 2 + 3;
в) на преобразование тригонометрических выражений: 2sin 2 x – 3cos 2 x + 4 = 5sin 2 x +1;
г) использование монотонности функции x 1/3 + 2 x-1 возрастает на R.
III. Рассмотрим способы нахождения областей значений функций.
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.
Раскроем суть этих методов на конкретных примерах.
Пример 1. Найдите область значений E(y) функции y = log 0,5 (4 – 2·3 x – 9 x).
Решим этот пример методом последовательного нахождения значений сложных аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
y = log 0,5 (5 – (1 + 2·3 x – 3 2x)) = log 0,5 (5 – (3 x + 1) 2)
И последовательно найдём множества значений её сложных аргументов:
E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)
Обозначим t = 5 – (3 x +1) 2 , где -∞≤t≤4 . Тем самым задача сводится к нахождению множества значений функции y = log 0,5 t на луче (-∞;4) . Так как функция y = log 0,5 t определена лишь при, то её множество значений на луче (-∞;4) совпадает со множеством значений функции на интервале (0;4), представляющем собой пересечение луча (-∞;4) с областью определения (0;+∞) логарифмической функции. На интервале (0;4) эта функция непрерывна и убывает. При t > 0 она стремится к +∞, а при t = 4 принимает значение -2, поэтому E(y) = (-2, +∞).
Пример 2. Найдите область значений функции
y = cos7x + 5cosx
Решим этот пример методом оценок, суть которого состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Из неравенств -1≤cos7x?1, -5≤5cosx?5 получим оценку -6≤y?6. При x = р и x = 0 функция принимает значения -6 и 6, т.е. достигает нижней и верхней границы оценки. Как линейная комбинация непрерывных функций cos7x и cosx, функция y непрерывна на всей числовой оси, поэтому по свойству непрерывной функции она принимает все значения с -6 до 6 включительно, и только их, так как в силу неравенств -6≤y?6 другие значения у неё невозможны. Следовательно, E(y) = [-6;6].
Пример 3. Найдите область значений E(f) функции f(x) = cos2x + 2cosx.
По формуле косинуса двойного угла преобразуем функция f(x) = 2cos 2 x + 2cosx – 1 и обозначим t = cosx. Тогда f(x) = 2t 2 + 2t – 1. Так как E(cosx) =
[-1;1], то область значений функции f(x) совпадает со множеством значений функции g(t) = 2t 2 + 2t – 1 на отрезке [-1;1], которое найдём графическим методом. Построив график функции y = 2t 2 + 2t – 1 = 2(t + 0,5) 2 – 1,5 на промежутке [-1;1], находим E(f) = [-1,5; 3].
Замечание – к нахождению множества значений функции сводятся многие задачи с параметром, связанные, в основном, с разрешимостью и числом решений уравнения и неравенств. Например, уравнение f(x) = а разрешимо тогда и только тогда, когда
a E(f) Аналогично, уравнение f(x) = а имеет хотя бы один корень, расположенный на некотором промежутке Х, или не имеет ни одного корня на этом промежутке тогда и только тогда, когда а принадлежит или не принадлежит множеству значений функции f(x) на промежутке Х. Также исследуются с привлечением множества значений функции и неравенства f(x)≠ а, f(x)> а и т.д. В частности, f(x)≠ а для всех допустимых значений х, если a E(f)
Пример 4. При каких значениях параметра а уравнение (x + 5) 1/2 = a(x 2 + 4) имеет единственный корень на отрезке [-4;-1].
Запишем уравнение в виде (x + 5) 1/2 / (x 2 + 4) = a . Последнее уравнение имеет хотя бы один корень на отрезке [-4;-1] тогда и только тогда, когда а принадлежит множеству значений функции f(x) = (x + 5) 1/2 / (x 2 + 4) на отрезке [-4;-1]. Найдём это множество, используя свойство непрерывности и монотонности функции.
На отрезке [-4;-1] функция y = xІ + 4 непрерывна, убывает и положительна, поэтому функция g(x) = 1 /(x 2 + 4) непрерывна и возрастает на этом отрезке, так как при делении на положительную функцию характер монотонности функции меняется на противоположный. Функция h(x) = (x + 5) 1/2 непрерывна и возрастает в своей области определения D(h) = [-5;+∞) и, в частности на отрезке [-4;-1], где она, кроме того, положительна. Тогда функция f(x)=g(x)·h(x) , как произведение двух непрерывных, возрастающих и положительных функций, также непрерывна и возрастает на отрезке [-4;-1], поэтому её множество значений на [-4;-1] есть отрезок [f(-4); f(-1) ] = . Следовательно, уравнение имеет решение на отрезке [-4;-1], причём единственное (по свойству непрерывной монотонной функции), при 0,05 ≤ a ≤ 0,4
Замечание. Разрешимость уравнения f(x) = a на некотором промежутке Х равносильна принадлежности значений параметра а множеству значений функции f(x) на Х. Следовательно, множество значений функции f(x) на промежутке Х совпадает с множеством значений параметра а , для которых уравнение f(x) = a имеет хотя бы один корень на промежутке Х. В частности, область значений E(f) функции f(x) совпадает с множеством значений параметра а , для которых уравнение f(x) = a имеет хотя бы один корень.
Пример 5. Найдите область значений E(f) функции
Решим пример методом введения параметра, согласно которому E(f) совпадает с множеством значений параметра а , для которых уравнение
имеет хотя бы один корень.
При а=2 уравнение является линейным – 4х – 5 = 0 с ненулевым коэффициентом при неизвестной х, поэтому имеет решение. При а≠2 уравнение является квадратным, поэтому оно разрешимо тогда и только тогда, когда его дискриминант
Так как точка а = 2 принадлежит отрезку
то
искомым множеством значений параметра а,
значит, и областью значений E(f)
будет весь отрезок.
Как непосредственное развитие метода введения параметра при нахождении множества значений функции, можно рассматривать метод обратной функции, для нахождения которой надо решить относительно х уравнение f(x)= y , считая y параметром. Если это уравнение имеет единственное решение x =g(y) , то область значений E(f) исходной функции f(x) совпадает с областью определения D(g) обратной функции g(y) . Если же уравнение f(x)= y имеет несколько решений x =g 1 (y) , x =g 2 (y) и т.д., то E(f) равна объединению областей определений функции g 1 (y), g 2 (y) и т.д.
Пример 6. Найдите область значений E(y) функции y = 5 2/(1-3x).
Из уравнения
найдём обратную функцию x = log 3 ((log 5 y – 2)/(log 5 y)) и её область определения D(x) :
Так как уравнения относительно х имеет единственное решение, то
E(y) = D(x) = (0; 1)(25;+∞ ).
Если область определения функции состоит из нескольких промежутков или функция на разных промежутках задана разными формулами, то для нахождения области значений функции надо найти множества значений функции на каждом промежутке и взять их объединение.
Пример 7. Найдите области значений f(x) и f(f(x)) , где
f(x) на луче (-∞;1], где она совпадает с выражением 4 x + 9·4 -x + 3. Обозначим t = 4 x . Тогда f(x) = t + 9/t + 3 , где 0 < t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x) на луче (-∞;1] совпадает с множеством значений функции g(t) = t + 9/t + 3 , на промежутке (0;4], которое найдём, используя производную g’(t) = 1 – 9/t 2 . На промежутке (0;4] производная g’(t) определена и обращается там в нуль при t = 3 . При 0<t <3 она отрицательна, а при 3<t <4 положительна. Следовательно, в интервале (0;3) функция g(t) убывает, а в интервале (3;4) она возрастает, оставаясь непрерывной на всём промежутке (0;4), поэтом g(3)= 9 – наименьшее значений этой функции на промежутке (0;4], в то время как её наибольшее значение не существует, так при t→0 справа функция g(t)→+∞. Тогда, по свойству непрерывной функции, множеством значений функции g(t) на промежутке (0;4], а значит, и множеством значений f(x) на (-∞;-1], будет луч .
Теперь, объединив промежутки – множества значений функции f(f(x)) , обозначим t = f(x) . Тогда f(f(x)) = f(t) , где При указанных t функция f(t) = 2cos(x-1) 1/2 + 7 и она снова принимает все значения от 5 до 9 включительно, т.е. область значений E(fІ) = E(f(f(x))) = .
Аналогично, обозначив z = f(f(x)) , можно найти область значений E(f 3) функции f(f(f(x))) = f(z) , где 5 ≤ z ≤ 9 и т.д. Убедитесь, что E(f 3) = .
Наиболее универсальным методом нахождения множества значений функции является использование наибольшего и наименьшего значений функции на заданном промежутке.
Пример 8. При каких значениях параметра р неравенcтво 8 x -р ≠ 2 x+1 – 2 x выполняется для всех -1 ≤ x < 2.
Обозначив t = 2 x , запишем неравенство в виде р ≠ t 3 – 2t 2 + t . Так как t = 2 x – непрерывная возрастающая функция на R, то при -1 ≤ x < 2 переменная
2 -1 ≤ t <2 2 ↔
0,5 ≤ t < 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда р отлична от значений функции f(t) = t 3 – 2t 2 + t при 0,5 ≤ t < 4.
Найдём сначала множество значений функции f(t) на отрезке , где она всюду имеет производную f’(t) =3t 2 – 4t + 1 . Следовательно, f(t) дифференцируема, значит, и непрерывна на отрезке . Из уравнения f’(t) = 0 найдём критические точки функции t = 1/3, t = 1, первая из которых не принадлежит отрезку , а вторая принадлежит ему. Так как f(0,5) = 1/8, f(1) = 0, f(4) = 36, то, по свойству дифференцируемой функции, 0 – наименьшее, а 36 – наибольшее значение функции f(t) на отрезке . Тогда f(t), как непрерывная функция, принимает на отрезке все значения от 0 до 36 включительно, причём значение 36 принимает только при t = 4 , поэтому при 0,5 ≤ t < 4, она принимает все значения из промежутка . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Пример 1
Условие: найдите область значений y = a r c sin x .
Решение
В общем случае область определения арксинуса располагается на отрезке [ - 1 ; 1 ] . Нам надо определить наибольшее и наименьшее значение указанной функции на нем.
y " = a r c sin x " = 1 1 - x 2
Мы знаем, что производная функции будет положительной для всех значений x , расположенных в интервале [ - 1 ; 1 ] , то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x , равном - 1 , а самое большое – при x , равном 1 .
m i n x ∈ - 1 ; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2
Таким образом, область значений функции арксинус будет равна E (a r c sin x) = - π 2 ; π 2 .
Ответ: E (a r c sin x) = - π 2 ; π 2
Пример 2
Условие: вычислите область значений y = x 4 - 5 x 3 + 6 x 2 на заданном отрезке [ 1 ; 4 ] .
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
y " = x 4 - 5 x 3 + 6 x 2 " = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12) = 0 x 1 = 0 ∉ 1 ; 4 и л и 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 · 4 · 12 = 33 x 2 = 15 - 33 8 ≈ 1 . 16 ∈ 1 ; 4 ; x 3 = 15 + 33 8 ≈ 2 . 59 ∈ 1 ; 4
Теперь найдем значения заданной функции в концах отрезка и точках x 2 = 15 - 33 8 ; x 3 = 15 + 33 8:
y (1) = 1 4 - 5 · 1 3 + 6 · 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 · 15 - 33 8 3 + 6 · 15 - 33 8 2 = = 117 + 165 33 512 ≈ 2 . 08 y 15 + 33 8 = 15 + 33 8 4 - 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 y (4) = 4 4 - 5 · 4 3 + 6 · 4 2 = 32
Значит, множество значений функции будет определяться отрезком 117 - 165 33 512 ; 32 .
Ответ: 117 - 165 33 512 ; 32 .
Перейдем к нахождению множества значений непрерывной функции y = f (x) в промежутках (a ; b) , причем a ; + ∞ , - ∞ ; b , - ∞ ; + ∞ .
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Пример 3
Условие: вычислите область значений функции y = 1 x 2 - 4 на интервале (- 2 ; 2) .
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
y " = 1 x 2 - 4 " = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2 ; 2)
У нас получилось максимальное значение, равное 0 , поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:
То есть y (0) = 1 0 2 - 4 = - 1 4 будет максимальным значений функции.
Теперь определим поведение функции при таком x, который стремится к - 2 с правой стороны и к + 2 с левой стороны. Иными словами, найдем односторонние пределы:
lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 · 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 · 1 - 0 = - ∞
У нас получилось, что значения функции будут возрастать от минус бесконечности до - 1 4 тогда, когда аргумент изменяется в пределах от - 2 до 0 . А когда аргумент меняется от 0 до 2 , значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (- ∞ ; - 1 4 ] .
Ответ: (- ∞ ; - 1 4 ] .
Пример 4
Условие : укажите множество значений y = t g x на заданном интервале - π 2 ; π 2 .
Решение
Нам известно, что в общем случае производная тангенса в - π 2 ; π 2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:
lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞
Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от - π 2 до π 2 ,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.
Ответ: - ∞ ; + ∞ .
Пример 5
Условие: определите, какова область значений функции натурального логарифма y = ln x .
Решение
Нам известно, что данная функция является определенной при положительных значениях аргумента D (y) = 0 ; + ∞ . Производная на заданном интервале будет положительной: y " = ln x " = 1 x . Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:
lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Пример 6
Условие: определите, какова область значений функции y = 9 x 2 + 1 .
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0
В итоге мы определили, что данная функция будет убывать, если x ≥ 0 ; возрастать, если x ≤ 0 ; она имеет точку максимума y (0) = 9 0 2 + 1 = 9 при переменной, равной 0 .
Посмотрим, как же ведет себя функция на бесконечности:
lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 · 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 · 1 + ∞ = + 0
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9 . Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0 . Мы отобразили это на рисунке:
На нем видно, что областью значений функции будет интервал E (y) = (0 ; 9 ]
Ответ: E (y) = (0 ; 9 ]
Если нам надо определить множество значений функции y = f (x) на промежутках [ a ; b) , (a ; b ] , [ a ; + ∞) , (- ∞ ; b ] , то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Пример 7
Условие: определите, какова будет область значений y = x x - 2 .
Решение
Поскольку знаменатель функции не должен быть обращен в 0 , то D (y) = - ∞ ; 2 ∪ 2 ; + ∞ .
Начнем с определения множества значений функции на первом отрезке - ∞ ; 2 , который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.
lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0
Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1 . Если же значения x меняются от минус бесконечности до 2 , то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала - ∞ ; 1 . Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0
Значения функции на данном отрезке определяются множеством 1 ; + ∞ . Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств - ∞ ; 1 и 1 ; + ∞ .
Ответ: E (y) = - ∞ ; 1 ∪ 1 ; + ∞ .
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Пример 8
Условие: определите область значений синуса y = sin x .
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z
В рамках 0 ; 2 π у функции будут точки экстремума π 2 и x = 3 π 2 . Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.
y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1 , max x ∈ 0 ; 2 π sin x = sin π 2 = 1
Ответ: E (sin x) = - 1 ; 1 .
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Пример 9
Условие: определите область значения y = 3 a r c cos x 3 + 5 π 7 - 4 .
Решение
Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E (a r c cos x) = 0 ; π или 0 ≤ a r c cos x ≤ π . Мы можем получить функцию a r c cos x 3 + 5 π 7 из арккосинуса, сдвинув и растянув ее вдоль оси O x , но такие преобразования нам ничего не дадут. Значит, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .
Функция 3 a r c cos x 3 + 5 π 7 может быть получена из арккосинуса a r c cos x 3 + 5 π 7 с помощью растяжения вдоль оси ординат, т.е. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Финалом преобразований является сдвиг вдоль оси O y на 4 значения. В итоге получаем двойное неравенство:
0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4
Мы получили, что нужная нам область значений будет равна E (y) = - 4 ; 3 π - 4 .
Ответ: E (y) = - 4 ; 3 π - 4 .
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Пример 10
Условие: вычислите, какова будет область значений функции y = 2 2 x - 1 + 3 .
Решение
Перепишем функцию, заданную в условии, как y = 2 · (2 x - 1) - 1 2 + 3 . Для степенной функции y = x - 1 2 область значений будет определена на промежутке 0 ; + ∞ , т.е. x - 1 2 > 0 . В таком случае:
2 x - 1 - 1 2 > 0 ⇒ 2 · (2 x - 1) - 1 2 > 0 ⇒ 2 · (2 x - 1) - 1 2 + 3 > 3
Значит, E (y) = 3 ; + ∞ .
Ответ: E (y) = 3 ; + ∞ .
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Пример 11
Условие: дана функция y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3 < x ≤ 3 1 x - 3 , x > 3 . Вычислите область ее значений.
Решение
Данная функция является определенной для всех значений x . Проведем ее анализ на непрерывность при значениях аргумента, равных - 3 и 3:
lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)
Имеем неустранимый разрыв первого рода при значении аргумента - 3 . При приближении к нему значения функции стремятся к - 2 sin 3 2 - 4 , а при стремлении x к - 3 с правой стороны значения будут стремиться к - 1 .
lim x → 3 - 0 f (x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f (x) = lim x → 3 + 0 1 x - 3 = + ∞
Имеем неустранимый разрыв второго рода в точке 3 . Когда функция стремится к нему, ее значения приближаются к - 1 , при стремлении к той же точке справа – к минус бесконечности.
Значит, вся область определения данной функции является разбитой на 3 интервала (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) .
На первом из них у нас получилась функция y = 2 sin x 2 - 4 . Поскольку - 1 ≤ sin x ≤ 1 , получаем:
1 ≤ sin x 2 < 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2
Значит, на данном промежутке (- ∞ ; - 3 ] множество значении функции – [ - 6 ; 2 ] .
На полуинтервале (- 3 ; 3 ] получилась постоянная функция y = - 1 . Следовательно, все множество ее значений в данном случае будет сводится к одному числу - 1 .
На втором промежутке 3 ; + ∞ у нас есть функция y = 1 x - 3 . Она является убывающей, потому что y " = - 1 (x - 3) 2 < 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:
lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0
Значит, множество значений исходной функции при x > 3 представляет собой множество 0 ; + ∞ . Теперь объединим полученные результаты: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; + ∞ .
Ответ: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; + ∞ .
Решение показано на графике:
Пример 12
Условие: есть функция y = x 2 - 3 e x . Определите множество ее значений.
Решение
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
y " = x 2 - 3 e x " = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x
Мы знаем, что производная обратится в 0 , если x = - 1 и x = 3 . Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.
Функция будет убывать на (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) и возрастать на [ - 1 ; 3 ] . Точкой минимума будет - 1 , максимума – 3 .
Теперь найдем соответствующие значения функции:
y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3
Посмотрим на поведение функции на бесконечности:
lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 " e x " = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x " (e x) " = 2 lim x → + ∞ 1 e x = 2 · 1 + ∞ = + 0
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
На нем видно, что значения функции будут убывать от плюс бесконечности до - 2 e тогда, когда аргумент меняется от минус бесконечности до - 1 . Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6 e - 3 до 0 , но при этом 0 достигнут не будет.
Таким образом, E (y) = [ - 2 e ; + ∞) .
Ответ: E (y) = [ - 2 e ; + ∞)
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Сегодня на уроке мы обратимся к одному из основных понятий математики - понятию функции; более детально рассмотрим одно из свойств функции - множество ее значений.
Ход урока
Учитель. Решая задачи, мы замечаем, что подчас именно нахождение множества значений функции ставит нас в затруднительные ситуации. Почему? Казалось бы, изучая функцию с 7-го класса, мы знаем о ней достаточно много. Поэтому у нас есть все основания сделать упреждающий ход. Давайте сегодня сами «поиграем» с множеством значений функции, чтобы снять многие вопросы этой темы на предстоящем экзамене.
Множества значений элементарных функций
Учитель. Для начала необходимо повторить графики, уравнения и множества значений основных элементарных функций на всей области определения.
На экран проецируются графики функций: линейной, квадратичной, дробно-рациональной, тригонометрических, показательной и логарифмической, для каждой из них устно определяется множество значений. Обратите внимание учащихся на то, что у линейной функции E(f) = R или одно число, у дробно-линейной
Это наша азбука. Присоединив к ней наши знания о преобразованиях графиков: параллельный перенос, растяжение, сжатие, отражение, мы сможем решить задачи первой части ЕГЭ и даже чуть сложнее. Проверим это.
Самостоятельная работа
Условия задач и системы координат напечатаны для каждого ученика .
1. Найдите множество значений функции на всей области определения:
а) y
= 3 sin х
;
б) y
= 7 – 2 х
;
в) y
= –arccos (x
+ 5):
г) y
= | arctg
x
|;
д)
2. Найдите множество значений функции y = x 2 на промежутке J , если:
а) J
= ;
б) J
= [–1; 5).
3. Задайте функцию аналитически (уравнением), если множество ее значений:
1) E (f (x )) = (–∞ ; 2] и f (x ) - функция
а) квадратичная,
б) логарифмическая,
в) показательная;
2) E (f (x )) = R \{7}.
При обсуждении задания 2 самостоятельной работы обратите внимание учащихся на то, что, в случае монотонности и непрерывности функции y = f (x ) на заданном промежутке [a ; b ], множество ее значений - промежуток , концами которого являются значения f (a ) и f (b ).
Варианты ответов к заданию 3.
1.
а) y
= –x
2 + 2 , y
= –(x
+ 18) 2 + 2,
y
= a
(x
– x
в) 2
+ 2 при а
< 0.
б) y = –| log 8 x | + 2,
в) y = –| 3 x – 7 | + 2, y = –5 | x | + 3.
2.
а)
б)
в) y = 12 – 5x , где x ≠ 1 .
Нахождение множества значений функции с помощью производной
Учитель. В 10-м классе мы знакомились с алгоритмом нахождения экстремумов непрерывной на отрезке функции и отыскания ее множества значений, не опираясь на график функции. Вспомните, как мы это делали? (С помощью производной .) Давайте вспомним этот алгоритм.
1. Убедиться, что функция y = f (x ) определена и непрерывна на отрезке J = [a ; b ]. 2. Найти значения функции на концах отрезка: f(a) и f(b). Замечание . Если мы знаем, что функция непрерывна и монотонна на J , то можно сразу дать ответ: E (f ) = [f (a ); f (b )] или E (f ) = [f (b ); f (а )]. 3. Найти производную, а затем критические точки x k J . 4. Найти значения функции в критических точках f (x k ). 5. Сравнить значения функции f (a ), f (b ) и f (x k ), выбрать наибольшее и наименьшее значения функции и дать ответ: E (f )= [f наим; f наиб ]. |
Задачи на применение данного алгоритма встречаются в вариантах ЕГЭ. Так, например, в 2008 году была предложена такая задача. Вам предстоит решить ее дома .
Задание С1. Найдите наибольшее значение функции
f (x ) = (0,5x + 1) 4 – 50(0,5x + 1) 2
при | x + 1| ≤ 3.
Условия домашних задач распечатаны для каждого ученика .
Нахождение множества значений сложной функции
Учитель. Основную часть нашего урока составят нестандартные задачи, содержащие сложные функции, производные от которых являются очень сложными выражениями. Да и графики этих функций нам неизвестны. Поэтому для решения мы будем использовать определение сложной функции, то есть зависимость между переменными в порядке их вложенности в данную функцию, и оценку их области значений (промежутка изменения их значений). Задачи такого вида встречаются во второй части ЕГЭ. Обратимся к примерам.
Задание 1. Для функций y = f (x ) и y = g (x ) записать сложную функцию y = f (g (x )) и найти ее множество значений:
а) f
(x
) = –x
2 + 2x
+
3, g
(x
) = sin x
;
б) f
(x
) = –x
2 + 2x
+
3, g
(x
) = log 7 x
;
в)
g
(x
) = x
2 + 1;
г)
Решение. а) Сложная функция имеет вид: y = –sin 2 x + 2sin x + 3.
Вводя промежуточный аргумент t , мы можем записать эту функцию так:
y = –t 2 + 2t + 3, где t = sin x .
У внутренней функции t = sin x аргумент принимает любые значения, а множество ее значений - отрезок [–1; 1].
Таким образом, для внешней функции y = –t 2 +2t + 3 мы узнали промежуток изменения значений ее аргумента t : t [–1; 1]. Обратимся к графику функции y = –t 2 +2t + 3.
Замечаем, что квадратичная функция при t [–1; 1] принимает наименьшее и наибольшее значения на его концах: y наим = y (–1) = 0 и y наиб = y (1) = 4. А так как эта функция непрерывна на отрезке [–1; 1], то она принимает и все значения между ними.
Ответ : y .
б) Композиция этих функций приводит нас к сложной функции которая после введения промежуточного аргумента, может быть представлена так:
y = –t 2 + 2t + 3, где t = log 7 x ,
У функции t = log 7 x
x (0; +∞ ), t (–∞ ; +∞ ).
У функции y = –t 2 + 2t + 3 (см. график) аргумент t принимает любые значения, а сама квадратичная функция принимает все значения не больше 4.
Ответ : y (–∞ ; 4].
в) Сложная функция имеет следующий вид:
Вводя промежуточный аргумент, получаем:
где t = x 2 + 1.
Так как для внутренней функции x R , а t .
Ответ : y (0; 3].
г) Композиция двух данных функций дает нам сложную функцию
которая может быть записана как
Заметим, что
Значит, при
где k Z , t [–1; 0) (0; 1].
Нарисовав график функции видим, что при этих значениях t
y (–∞ ; –4] c ;
б) на всей области определения.
Решение. Вначале исследуем данную функцию на монотонность. Функция t = arcctg x - непрерывная и убывающая на R и множество ее значений (0; π). Функция y = log 5 t определена на промежутке (0; π), непрерывна и возрастает на нем. Значит, данная сложная функция убывает на множестве R . И она, как композиция двух непрерывных функций, будет непрерывна на R .
Решим задачу «а».
Так как функция непрерывна на всей числовой оси, то она непрерывна и на любой ее части, в частности, на данном отрезке. А тогда она на этом отрезке имеет наименьшее и наибольшее значения и принимает все значения между ними:
f (4) = log 5 arcctg 4.
Какое из полученных значений больше? Почему? И каким же будет множество значений?
Ответ: 
Решим задачу «б».
Ответ: у (–∞ ; log 5 π) на всей области определения.
Задача с параметром
Теперь попробуем составить и решить несложное уравнение с параметром вида f (x ) = a , где f (x ) - та же функция, что и в задании 4.
Задание 5. Определите количество корней уравнения log 5 (arcctg x ) = а для каждого значения параметра а .
Решение. Как мы уже показали в задании 4, функция у = log 5 (arcctg x ) - убывает и непрерывна на R и принимает значения меньше log 5 π. Этих сведений достаточно, чтобы дать ответ.
Ответ: если а < log 5 π, то уравнение имеет единственный корень;
если а ≥ log 5 π, то корней нет.
Учитель. Сегодня мы рассмотрели задачи, связанные с нахождением множества значений функции. На этом пути мы открыли для себя новый метод решения уравнений и неравенств - метод оценки, поэтому нахождение множества значений функции стало средством решения задач более высокого уровня. При этом мы увидели, как конструируются такие задачи и как свойства монотонности функции облегчают их решение.
И мне хочется надеяться, что та логика, которая связала рассмотренные сегодня задачи, вас поразила или хотя бы удивила. Иначе и быть не может: восхождение на новую вершину никого не оставляет равнодушным! Мы замечаем и ценим красивые картины, скульптуры и т.д. Но и в математике есть своя красота, притягивающая и завораживающая - красота логики. Математики говорят, что красивое решение - это, как правило, правильное решение, и это не просто фраза. Теперь Вам самим предстоит находить такие решения и один из путей к ним мы указали сегодня. Удачи вам! И помните: дорогу осилит идущий!
